Pentru ce combinații este importantă ordinea elementelor? Formule combinatorice

Sarcină . Determinați numărul tuturor seturilor ordonate lungime r, care poate fi compus din elemente ale ansamblului X (
), dacă selectarea fiecărui element
, este produs din întregul set X.

Set comandat
este un element al produsului cartezian
, constând din r multiplicatori identici X. Conform regulii produsului, numărul de elemente ale unui set
egală
. Am derivat formula
.

Exemplu. Câte numere de telefon din patru cifre pot fi făcute folosind toate cele zece cifre?

Aici
, iar numărul de numere de telefon este

2.1.5. Plasări fără repetări

Sarcină . Câte seturi comandate
poate fi compus din n elemente ale ansamblului X, dacă toate elementele setului sunt diferite?

Primul element Poți alege n moduri. Dacă primul element este deja selectat, atunci al doilea element poti doar sa alegi
moduri și dacă este deja selectat
element
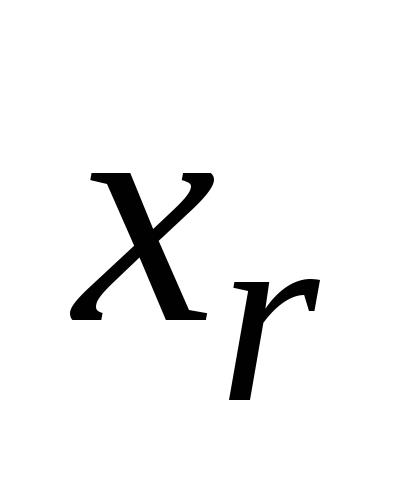, apoi elementul Poți alege
modalități (repetarea unui element deja selectat nu este permisă). Prin regula produsului obținem

Această formulă este scrisă diferit folosind notația
. Deoarece

.

Exemplu. Câte liste diferite de câștigători ai olimpiadelor pot exista (primul, al doilea, al treilea) dacă au participat 20? Uman?

Aici
, numărul necesar este

2.1.6. Permutări fără repetare

Să luăm în considerare un caz special de plasare fără repetări: dacă
, atunci toate elementele setului participă la plasare X, adică probele au aceeași compoziție și diferă între ele doar în ordinea elementelor. Astfel de mostre sunt numite permutări . Numărul de permutări de la n elementele reprezintă :

Exemplu.În câte moduri vă puteți alinia la casa de marcat dacă șase persoane vor să fie plătite?

2.1.7. Permutări cu repetări

Lasă decorul X cuprinde k diverse elemente:
.Permutarea cu repetări compoziţie
vom numi un set ordonat de lungime
, în care elementul se intalneste o singura data
. Numărul de astfel de permutări este notat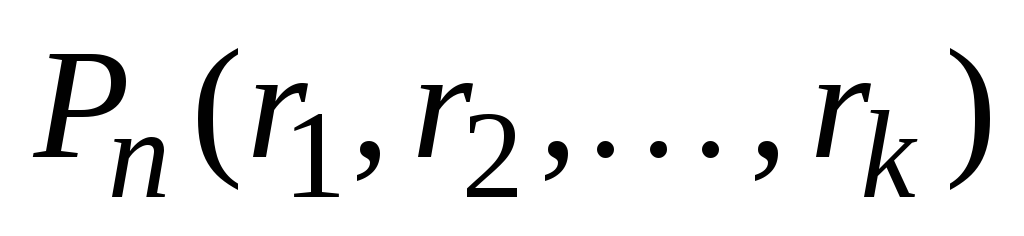
.

Exemplu. Din scrisori
să scriem o permutare cu repetare a compoziției
. Lungimea sa
, și scrisoarea A intra de 2 ori, b- de 2 ori, c- o singura data. O astfel de permutare ar fi, de exemplu,
sau
.

Să derivăm formula pentru numărul de permutări cu repetări. Să numerotăm toate elementele identice incluse în permutare cu indici diferiți, i.e. în loc de rearanjare
primim
. Acum toate elementele permutării sunt diferite, iar numărul acestor permutări este egal cu
. Primul element apare în probă o singura data. Să eliminăm indicii din primul element (în exemplul nostru obținem permutarea
), în timp ce numărul de permutări diferite va scădea cu ori, pentru că dacă schimbăm ordinea elementelor identice, eșantionul nostru nu se va schimba. Dacă eliminăm indicii din al doilea element, numărul de permutări va scădea cu o singura data. Și tot așa, până la elementul cu număr k– numărul de permutări va scădea cu o singura data. Primim formula

Exemplu. Câte „cuvinte” diferite puteți obține prin rearanjarea literelor cuvântului „transmitere”?

În acest cuvânt, literele „e” și „a” apar de două ori, restul o dată fiecare. Vorbim despre rearanjare cu repetare a compoziției
lungime. Numărul de astfel de permutări este egal cu

2.1.8. Combinații

Sarcină . Câte seturi diferite de r elementele pot fi compuse dintr-un set care contine n elemente?

Vom compune mai întâi seturi ordonate de r elemente din fiecare. Numărul de astfel de seturi (acestea sunt destinații de plasare din n elemente prin r) egal
. Acum luăm în considerare că ordinea în care sunt scrise elementele nu contează pentru noi. În același timp, din plasări diferite, care diferă doar în ordinea elementelor, obținem o combinație. De exemplu, două destinații de plasare diferite
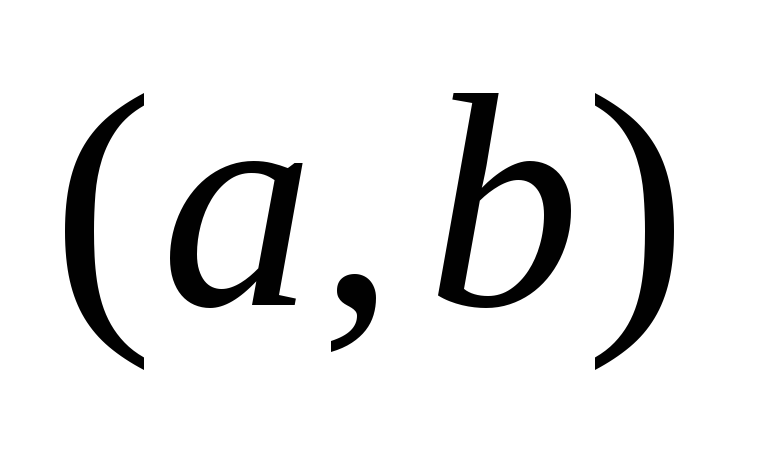Și
a două elemente corespund unei combinații
. Astfel, numărul de combinații V ori mai mic decât numărul de plasări :

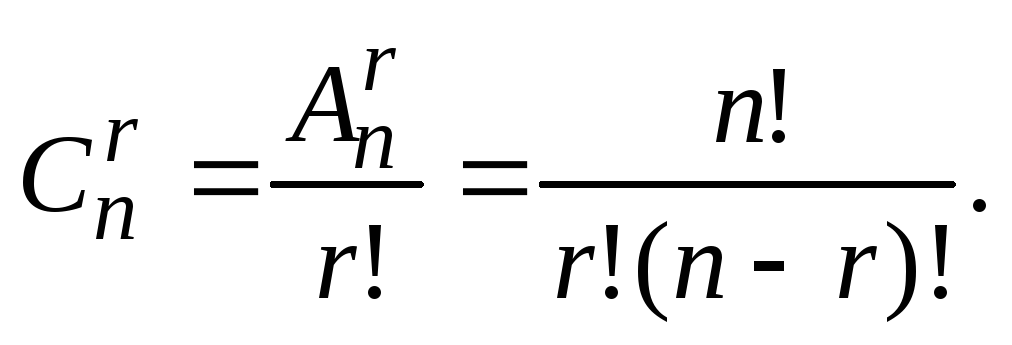
Exemplu. Numărul de moduri în care putem alege trei dintre cele opt ștergătoare este

O permutare este o combinație de elemente din N diferite elemente luate într-o anumită ordine. Într-o rearanjare, ordinea elementelor este importantă, iar toate elementele trebuie să fie implicate în rearanjare. N elemente.

Sarcină: Găsiți toate permutările posibile pentru succesiunea numerelor 1, 2, 3.
Există următoarele permutări:

1: 1 2 3
2: 1 3 2
3: 2 1 3
4: 2 3 1
5: 3 1 2
6: 3 2 1

Permutări fără repetare

Numărul de permutări pentru N elemente diferite este N!. Într-adevăr:

• Oricare dintre ele poate fi plasat pe primul loc N elemente (opțiuni totale N),
• oricare dintre cele rămase pot fi plasate în a doua poziţie (N-1) elemente (opțiuni totale N·(N-1)),
• dacă continuăm această secvență pentru toată lumea N locuri, obținem: N·(N-1)·(N-2)· … ·1, adică în total N! permutări.

Luați în considerare problema obținerii tuturor permutărilor numerelor 1…N(adică secvențe de lungime N), unde fiecare număr apare exact o dată. Există multe opțiuni pentru ordinea în care sunt obținute permutările. Cu toate acestea, problema cel mai frecvent rezolvată este generarea de permutări în lexicografic comanda (vezi exemplul de mai sus). În acest caz, toate permutările sunt sortate mai întâi după primul număr, apoi după al doilea etc. în ordine crescătoare. Deci prima va fi permutarea 1 2…N, Și ultimul - N N-1…1.

Să luăm în considerare un algoritm pentru rezolvarea problemei. Este dată șirul original de numere. Pentru a obține fiecare permutare ulterioară, trebuie să efectuați următorii pași:

• Este necesar să se uite prin permutarea curentă de la dreapta la stânga și, în același timp, să se asigure că fiecare element ulterior al permutării (elementul cu un număr mai mare) nu este mai mult decât cel anterior (elementul cu un număr mai mic) . De îndată ce acest raport este încălcat, trebuie să vă opriți și să marcați numărul curent (poziția 1).
• Revedeți calea parcursă din nou de la dreapta la stânga până ajungem la primul număr, care este mai mare decât cel marcat în pasul anterior.
• Schimbați cele două elemente rezultate.
• Acum, în partea matricei care se află în dreapta poziției 1, trebuie să sortați toate numerele în ordine crescătoare. Deoarece înainte de aceasta, toate erau deja scrise în ordine descrescătoare, este necesar să se răstoarne pur și simplu această parte a subsecvenței.

Astfel vom obține o nouă secvență, care va fi considerată ca fiind cea inițială în pasul următor.

Implementare în C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

#include
folosind namespace std;

{
int s = a[i];
a[i] = a[j];
a[j] = s;
}
bool NextSet(int *a, int n)
{
int j = n - 2;
în timp ce (j != -1 && a[j] >= a) j--;
dacă (j == -1)
returnează fals; // nu mai sunt permutări
int k = n - 1;
în timp ce (a[j] >= a[k]) k--;
swap(a, j, k);
int l = j + 1, r = n - 1;
în timp ce (l swap(a, l++, r--);
returnează adevărat;
}
void Print(int *a, int n) // ieșirea permutării
{
static int num = 1; // număr de permutare
cout.width(3);
cout<< num++ << ": " ;
pentru (int i = 0; i< n; i++)
cout<< a[i] << " " ;
cout<< endl;
}
int main()
{
int n, *a;
cout<< "N = " ;
cin >> n;
a = nou int[n];
pentru (int i = 0; i< n; i++)
a[i] = i + 1;
Print(a, n);
în timp ce (NextSet(a, n))
Print(a, n);
cin.get(); cin.get();
întoarce 0;
}

Rezultatul executiei

Permutări cu repetări

Problema generării permutărilor merită o atenție specială N elemente în cazul în care elementele secvenței pot fi repetate. Să presupunem că secvența originală este formată din elemente n 1 , n 2 ... n k, unde element n 1 se repetă r 1 o singura data, n 2 se repetă r 2 ori, etc. în care n 1 +n 2 +...+n k =N. Dacă numărăm totul n 1 +n 2 +...+n k elemente ale unei permutări cu repetări diferite, atunci în total există diferite variante de permutări ( n 1 +n 2 +...+n k)!. Cu toate acestea, printre aceste permutări, nu toate sunt diferite. De fapt, totul r 1 elemente n 1 putem schimba locurile unul cu celălalt, iar acest lucru nu va schimba permutarea. În același mod, putem rearanja elementele n 2, n 3 etc. Ca urmare avem r 1! opțiuni pentru scrierea aceleiași permutări cu aranjamente diferite de elemente repetate n 1. Astfel, orice permutare poate fi scrisă r 1 !·r 2 !·...·r k ! moduri. Prin urmare, numărul de permutări diferite cu repetări este egal cu

Pentru a genera permutări cu repetări, puteți utiliza algoritmul de generare a permutărilor fără repetări prezentat mai sus. Să introducem un element care se repetă în tabloul a. Mai jos este codul programului pentru generarea de permutări cu repetiții (se modifică doar codul funcției main()).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

#include
folosind namespace std;
void swap (int *a, int i, int j)
{
int s = a[i];
a[i] = a[j];
a[j] = s;
}
bool NextSet(int *a, int n)
{
int j = n - 2;
în timp ce (j != -1 && a[j] >= a) j--;
dacă (j == -1)
returnează fals; // nu mai sunt permutări
int k = n - 1;
în timp ce (a[j] >= a[k]) k--;
swap(a, j, k);
int l = j + 1, r = n - 1; // sortează restul secvenței
în timp ce (l swap(a, l++, r--);
returnează adevărat;
}
void Print(int *a, int n) // ieșirea permutării
{
static int num = 1; // număr de permutare
cout.width(3); // lățimea câmpului de ieșire al numărului de permutare
cout<< num++ << ": " ;
pentru (int i = 0; i< n; i++)
cout<< a[i] << " " ;
cout<< endl;
}
int main()
{
int n, *a;
cout<< "N = " ;
cin >> n;
a = nou int[n];
pentru (int i = 0; i< n; i++)
a[i] = i + 1;
a = 1; // element repetat
Print(a, n);
în timp ce (NextSet(a, n))
Print(a, n);
cin.get(); cin.get();
întoarce 0;
}

Rezultatul algoritmului de mai sus:

Plan:

1. Elemente de combinatorie.

2. Reguli generale de combinatorie.

4. Aplicarea graficelor (schemelor) în rezolvarea problemelor combinatorii.

Combinatorică este un domeniu al matematicii în care se studiază întrebări despre câte combinații diferite, supuse anumitor condiții, se pot face din elemente aparținând unei mulțimi date.

Combinatoria a apărut în secolul al XVI-lea. Jocurile de noroc (cărți, zaruri) ocupau un loc important în viața straturilor privilegiate ale societății la acea vreme. Loteriile erau răspândite. Inițial, problemele combinatorii se ocupau în principal de jocurile de noroc: în câte moduri se pot obține un anumit număr de puncte aruncând 2 sau 3 zaruri, sau în câte moduri se pot obține 2 regi într-un anumit joc de cărți. Acestea și alte probleme ale jocurilor de noroc au fost forța motrice în dezvoltarea combinatoriei și în continuare în dezvoltarea teoriei probabilităților.

Unul dintre primii care a numărat numărul de combinații diferite atunci când a jucat zaruri a fost matematicianul italian Tartaglia. El a compilat tabele (numărul de moduri de a obține k puncte pe r zaruri). Cu toate acestea, nu a ținut cont de faptul că aceeași cantitate de puncte poate cădea în moduri diferite, așa că tabelele sale conțineau un număr mare de erori.

Studiul teoretic al problemelor de combinatorie a fost întreprins în secolul al XVII-lea de către matematicienii francezi Blaise Pascal și Fermat. Punctul de plecare al cercetării lor au fost, de asemenea, problemele legate de jocurile de noroc.

Dezvoltarea ulterioară a combinatoriei este asociată cu numele lui J. Bernoulli, G. Leibniz, L. Euler. Cu toate acestea, în activitatea lor, aplicațiile la diferite jocuri au jucat un rol major.

Astăzi, metodele combinatorii sunt folosite pentru a rezolva problemele de transport, în special problemele de programare, pentru a întocmi planuri de producție și vânzări de produse etc.

Regula sumei: Dacă un obiect A poate fi ales în m moduri, iar un obiect B în k moduri, atunci obiectul „fie A fie B” poate fi ales în m + k moduri.

Exemple:

1. Să presupunem că într-o cutie există n bile de culori diferite. 1 minge este scoasă la întâmplare. În câte moduri se poate face acest lucru?

Răspuns: n moduri.

Să distribuim aceste n bile în două cutii: prima conține m bile, a doua conține k bile. 1 minge este extrasă aleatoriu dintr-o cutie aleasă aleatoriu. În câte moduri se poate face acest lucru?

Soluţie: Mingea poate fi scoasă din prima casetă în m moduri, iar din a doua în k moduri. Atunci numărul total de căi este m+k=n.

În semaforul maritim, fiecare literă a alfabetului corespunde unei anumite poziții a două steaguri în raport cu corpul semnalizatorului. Câte astfel de semnale pot exista?

Soluţie: Numărul total este suma pozițiilor când ambele steaguri sunt situate pe părți opuse ale corpului semnalizatorului și a pozițiilor când sunt situate pe aceeași parte a corpului semnalizatorului. La numărarea numărului de poziții posibile se aplică regula sumei.

Regula produsului: Dacă obiectul A poate fi selectat în m moduri, iar după fiecare astfel de alegere poate fi selectat un alt obiect B (indiferent de alegerea obiectului A) în k moduri, atunci perechile de obiecte „A și B” pot fi selectate în m * k moduri.

Exemple:

Soluţie: Numărul zecilor poate fi notat cu orice număr de la 1 la 9. Numărul unilor poate fi notat cu orice număr de la 0 la 9. Dacă numărul zecilor este 1, atunci numărul unilor poate fi orice număr (de la 0 la 9). Astfel, există 10 numere din două cifre, numărul zecilor fiind 1. Raționăm în mod similar pentru orice alt număr de zeci. Apoi putem calcula că sunt 9 *10 = 90 de numere din două cifre.

2. Sunt 2 sertare. Unul conține m cuburi multicolore, iar celălalt conține k bile multicolore. În câte moduri poți alege perechea „Cub-Ball”?

Soluţie: Alegerea mingii nu depinde de alegerea cubului și invers. Prin urmare, numărul de moduri în care o pereche dată poate fi selectată este m *k .

Populație fără repetări este o mulțime de un număr finit de elemente diferite a 1, a 2, a 3, ..., a n.

Exemplu: Set de n bucăți multicolore.

Volumul de eșantionarek (kn) este un grup de m elemente ale unei populații date.

Exemplu: O panglică pestriță cusută din m resturi multicolore selectate din n .

Postari de lan elemente fiecarek astfel de eșantioane se numesc acelea care conțin k elemente fiecare, selectate dintre cele n elemente date ale populației generale fără repetare și diferă unele de altele fie prin compoziția elementelor, fie prin ordinea aranjamentului lor.

- numărul de plasări de la n prin k.

Numărul de plasări de la n prin k poate fi determinată în felul următor: se poate selecta primul obiect de selecție n moduri, atunci al doilea obiect poate fi selectat n -1 cale etc.

Transformând această formulă, avem:

Trebuie amintit că 0!=1.

Exemple:

1. Sunt 17 echipe care participă în prima grupă din clasa A a campionatului de fotbal. Se acordă medalii: aur, argint și bronz. În câte moduri pot fi jucate?

Soluţie:Combinațiile de echipe câștigătoare diferă unele de altele prin compoziția și ordinea elementelor, adică. sunt plasamente de la 17 la 3.

2. Societatea științifică este formată din 25 de persoane. Este necesar să se aleagă un președinte al societății, un vicepreședinte, un secretar științific și un trezorier. În câte moduri se poate face acest lucru?

Soluţie: Combinațiile echipei de conducere a unei companii diferă unele de altele prin compoziția și ordinea elementelor, adică sunt plasamente de la 25 la 4.

Permutări fără repetări din nelementese numesc plasamente fara repetitii din n elemente ale lui n , adică plasamentele diferă între ele numai în ordinea elementelor.

Numărul de permutări.

Exemple:

1. Câte numere diferite din cinci cifre pot fi făcute din cifrele 1, 2, 3, 4, 5, cu condiția ca acestea să fie formate din cifre diferite?

Combinatii fara repetari din nelemente prink astfel de eșantioane se numesc acelea care conțin k elemente fiecare, selectate dintre cele n elemente date ale populației generale fără repetare și diferă unele de altele doar prin compoziția elementelor.

- numărul de combinații de n prin k

1. Dacă la semifinala unui campionat de șah participă 20 de persoane și doar trei ajung în finală, atunci în câte moduri pot fi determinate aceste trei?

Soluţie:În acest caz, ordinea în care se află acest triplu nu este semnificativă. Prin urmare, tripletele care au ajuns în finală sunt combinații de 20 de 3.

Soluţie:În acest caz, ordinea în care se află acest triplu nu este semnificativă. Prin urmare, tripleții de delegați sunt combinații de 10 cu 3.

Abstract:

4.Utilizarea graficelor (schemelor) în rezolvarea problemelor combinatorii.

În cazul în care numărul de opțiuni posibile la fiecare pas depinde de elementele selectate mai devreme, procesul de compunere a combinațiilor poate fi descris ca un „arboresc”. În primul rând, sunt trase atâtea segmente dintr-un punct câte alegeri diferite pot fi făcute la primul pas. De la sfârșitul fiecărui segment, desenați cât mai multe segmente pot fi selectate la a doua etapă, dacă acest element a fost selectat la primul pas etc.

Sarcină:

La compilarea comenzilor navei spațiale, se ia în considerare și problema compatibilității psihologice a participanților la călătorie. Este necesar să alcătuiți un echipaj al navei spațiale de 3 persoane: un comandant, un inginer și un medic. Există 4 candidați pentru funcția de comandant: a 1 , a 2 , a 3 , a 4 .În locul inginerului 3:b 1, b 2, b 3. Pentru locul medicului - 3: c 1, c 2, c 3. Inspecția a arătat că comandantula 1 este compatibil psihologic cu inginerii b 1 și b 3și medicii c 1 și c 3. Comandant a 2 - cu ingineri b 1 și b 2 . si toti doctorii. Comandanta 3 - cu inginerib 1 și b 2 si doctoric 1 și c 3. Comandant a 4 - cu toti inginerii si doctorul c 2 . În plus, inginerb 1 incompatibil cu medicul c 3, b 2 - cu un medic c 1 și b 3 - cu un medic c 2. În câte moduri poate fi compus echipajul navei în aceste condiții?

Soluţie:

Să creăm „arborele” corespunzător.

Răspuns: 10 combinatii.

Un astfel de arbore este un grafic și este folosit pentru a rezolva probleme combinatorii.

Scopul lecției: să fie capabil să aplice formule de combinatorie de bază și să cunoască condițiile de aplicare a acestor formule; să cunoască proprietățile coeficienților binomi și să fie capabil să determine expansiunea unui binom pentru valori specifice ale lui n.

Planul lecției:

1. Numărul de plasări.

2. Numărul de permutări.

3. Numărul de combinații.

4. Repetări.

5. Binomul lui Newton. triunghiul lui Pascal.

Orientări pentru studierea temei

În multe cazuri practice, devine necesară numărarea numărului de combinații posibile de obiecte care îndeplinesc anumite condiții. Astfel de probleme se numesc combinatorii. Varietatea problemelor combinatorii nu poate fi descrisă exhaustiv, dar printre ele există o serie de probleme deosebit de comune pentru care sunt cunoscute metode de calcul.

Combinatorică- un domeniu al matematicii in care se studiaza intrebari despre cate combinatii diferite, supuse anumitor conditii, se pot face din elemente apartinand unei multimi date. Termenul „combinatorics” provine din cuvântul latin combina - a combina, a conecta.

Fie o mulțime de n elemente: x 1, x 2, x 3, ..., x n.

Din această mulțime se pot forma diverse submulțimi, adică eșantioane, fiecare dintre ele conține m elemente (0 ≤ m ≤ n). Există selecții ordonate (plasamente), permutări și selecții neordonate (combinații).

Plasări

Plasări n diverse elemente conform m elemente care diferă fie în alcătuirea elementelor, fie în ordinea acestora.

Numărul de plasări de la n elemente prin m elementele sunt desemnate (A este prima literă a aranjamentului cuvântului francez, ceea ce înseamnă plasare, punere în ordine) și se calculează folosind formula:

Conceptul de factorial

Muncă n numere naturale de la 1 la n indicat prin simbol n! (n factorial), adică

De exemplu, 2!=

5!=

Rețineți că este convenabil să se calculeze 0!, presupunând, prin definiție, 0!=1.

Exemple:

Din ultimele două formule rezultă că

Exemplu.

8 echipe participă la un turneu de fotbal dintr-o rundă. Câte opțiuni există pentru primii trei?

Soluţie: Deoarece ordinea echipelor din primele trei este importantă, avem de-a face cu plasamente. Apoi

(Opțiuni).

Exemplu.

În câte moduri pot fi selectate trei persoane din zece candidați pentru trei posturi diferite?

Soluţie:

(cai).

Exemplu.

Câte numere de telefon pot fi compuse din 5 cifre, astfel încât în ​​fiecare număr individual toate cifrele să fie diferite?

(numere de telefon).

Rearanjamente

Permutări sunt combinatii formate din aceleasi n elemente diferite şi diferind doar în ordinea dispunerii lor.

Numărul tuturor permutărilor posibile ale n elemente este notat cu P n (P este prima literă a cuvântului francez permutare, care înseamnă permutare) și se calculează folosind formula:

Exemplu.

8 sportivi concurează în finala de 100 de metri. Câte opțiuni de protocol de cursă există?

Soluţie:

În acest caz vorbim despre toate permutările a 8 elemente. Apoi (opțiuni)

Exemplu.

În câte moduri diferite pot sta 10 persoane pe o bancă?

Soluţie:

(cai)

Exemplu.

În câte moduri pot fi așezate 7 persoane la o masă cu 7 tacâmuri?

Soluţie:

(cai).

Combinații

Combinații sunt combinatii realizate din n diverse elemente conform m elemente care diferă în cel puțin un element.

Numărul de combinații se calculează folosind formula: (C este prima literă a combinației de cuvinte franceze).

Exemplu.

În câte moduri pot fi selectate trei persoane pentru trei posturi identice din zece candidați?

Soluţie:

(cai).

Exemplu.

În câte moduri puteți selecta trei părți dintr-o cutie care conține 15 părți?

Soluţie:

(cai).

Un alt tip de formulă pentru numărul de plasări și numărul de combinații

; , acesta este .

Proprietățile numărului de combinații:

5)

La rezolvarea problemelor de combinatorie se folosesc următoarele reguli:

Regula sumei. Dacă un obiect A poate fi selectat dintr-un set de obiecte în n moduri și un alt obiect B - în k moduri, atunci obiectul „fie A, fie B” poate fi selectat în n + k moduri.

Regula produsului. Dacă un anumit obiect A poate fi selectat dintr-un set de obiecte în n moduri și după fiecare astfel de selecție un alt obiect B în k moduri, atunci o pereche de obiecte (A, B) în ordinea specificată poate fi selectată în n × k moduri .

Dacă unele elemente sunt repetate, atunci în acest caz combinațiile cu repetări sunt calculate folosind alte formule.

Plasări cu repetări

Numărul de plasări după m elemente cu repetari din n elemente diferite sunt egale n m,acesta este

Exemplu.

Din numerele 1,2,3,4,5, puteți face 5 3 = 125 de numere din trei cifre, dacă același număr poate conține aceleași numere.

Permutări cu repetări

Dacă printre n sunt elemente n 1 elemente de același tip, n 2 elemente de alt tip etc., apoi numărul de permutări cu repetări

Unde

Exemplu.

Câte permutări diferite de litere pot fi făcute în cuvântul „matematică”?

Soluţie:

Combinații cu repetări

Numărul de combinații cu repetări de la n diverse elemente conform m elemente este egal cu numărul de combinații fără repetări de la ( n+m-1) diverse elemente conform m elemente:

Exemplu.

Aflați numărul de combinații cu repetări a patru elemente A, b, c, d 3 elemente fiecare.

Soluţie:

Numărul necesar va fi

Teorema binomială

Pentru un număr întreg pozitiv arbitrar n, următoarea formulă este valabilă:

Acesta este binomul lui Newton. Coeficienții se numesc coeficienți binomiali.

Pentru n = 2 obținem formula;

Pentru n = 3 obținem formula.

Exemplu. Determinați expansiunea pentru n=4.

Soluţie:

Coeficienții binomi au o serie de proprietăți:

2. ;

Luați în considerare următorul triunghi:

………………………….

Linia numerotată n conține coeficienți de expansiune binomială. Profitand de proprietate , puteți observa că fiecare element intern al triunghiului este egal cu suma celor două elemente situate deasupra acestuia, iar elementele laterale ale triunghiului sunt egale cu unitățile:

……………………….

Acesta este triunghiul lui Pascal. Vă permite să găsiți rapid valorile coeficienților binomi.

În literatura de limbă rusă, permutațiile compuse din n elemente diferite prin alegerea a m elemente care diferă fie în compoziția elementelor, fie în ordinea lor sunt de obicei numite plasări, iar permutările sunt înțelese ca întregul set de combinații constând din același n diferite. elemente şi diferă doar în ordinea amplasărilor lor. În acest sens, numărul tuturor permutărilor posibile pentru o mulțime de n elemente diferite este calculat folosind formula factorială Pn = n! sau în Excel „=FACT(N)” (vezi Fig. Nr. 1)

De exemplu, dacă introduceți „=PERST(3;2)”, obținem 6. Acestea sunt 6 combinații: (1,2), (2,1), (1,3), (3,1), ( 2,3) , (3,2).

Dar funcția încorporată „=NUMBERCOMB(N;K)” produce o formulă combinatorie, pe care o numim „Număr de combinații”. În literatura în limba rusă, acesta este numele pentru permutările formate din n elemente diferite prin alegerea a m elemente fiecare, care diferă numai în compoziția elementelor, iar ordinea selecției lor este indiferentă (a se vedea figura, nr. 4)

Când utilizați funcții încorporate, utilizați Ajutor pentru această funcție. De exemplu:

Probleme de rezolvat independent

1. Calculați:

2. Calculați:

3. Calculați:

4. Găsiți n, dacă 5С n 3 =

5. Găsiți n, Dacă

6. Găsiți n, Dacă

7. Găsiți n, Dacă

8. Găsiți n, Dacă ,kn

9. Rezolvați ecuația

10. Rezolvați sistemul

11. Câte semnale poți face din 6 steaguri de culori diferite, luate în grupuri de câte 2?

12. În câte moduri pot fi selectate patru persoane pentru patru posturi diferite din nouă candidați?

13. Câte numere de telefon pot fi compuse din 6 cifre astfel încât în ​​fiecare număr individual toate cifrele să fie diferite?

14. Există 10 materii academice și 5 lecții diferite pe zi în clasă. În câte moduri pot fi distribuite lecțiile într-o singură zi?

15. Câte numere din patru cifre poți scrie folosind toate cele 10 cifre fără a le repeta?

16. O companie selectează dintre nouă candidați pentru trei poziții diferite. Câte moduri există de a face această alegere?

17. În clasa a VIII-a se studiază 15 materii. În câte moduri poți crea un program pentru miercuri dacă știi că ar trebui să fie 6 lecții în acea zi?

18. În prima ligă a campionatului național de fotbal sunt 16 echipe. Lupta este pentru medalii de aur, argint și bronz. În câte moduri pot fi împărțite medaliile între echipe?

19. În câte moduri pot fi așezate 9 persoane la o masă cu 9 tacâmuri?

20. La întâlnire vor lua cuvântul 6 vorbitori. În câte moduri pot fi aranjate numele lor în listă?

21. Câte numere din trei cifre pot fi făcute din cifrele 1, 2, 3 dacă fiecare cifră apare în imaginea numărului o singură dată?

22. În câte moduri diferite pot fi aranjate 10 cărți diferite pe un raft astfel încât anumite 4 cărți să stea una lângă alta?

23. 8 echipe participă la un turneu de fotbal dintr-o rundă. Câte meciuri se vor juca?

24. Din 25 de studenți, trei delegați trebuie să fie selectați pentru conferință. În câte moduri se poate face acest lucru?

25. În câte moduri puteți selecta două părți dintr-o cutie care conține 10 părți?

26. Există 36 de cărți în pachet, dintre care 4 sunt ași. În câte moduri pot fi extrase 6 cărți astfel încât să fie 2 ași printre ele?

27. O echipă complexă este formată din doi zugravi, trei tencuitori și un tâmplar. Câte echipe diferite pot fi create dintr-o echipă de lucru formată din 15 zugravi, 10 tencuitori și 5 dulgheri?

28. 10 echipe participă la turneul de calificare pentru 3 bilete la Campionatul Mondial. Câte variante ale „trei norocoși” există?

29. Din 12 persoane, patru sunt selectate pentru a fi numiți în 4 posturi identice. În câte moduri se poate face o astfel de alegere?

30. În câte moduri diferite poate fi compus un grup de recunoaștere de 3 soldați și un comandant dacă sunt 12 soldați și 3 comandanți?

31. Dat în avion n puncte dintre care trei nu se află pe aceeași linie. Aflați numărul de drepte care pot fi obținute prin conectarea punctelor în perechi.

32. Literele codului Morse sunt formate ca o succesiune de puncte și liniuțe. Câte litere diferite pot fi formate folosind 5 simboluri?

33. Câte numere de telefon diferite din șapte cifre există?

34. Să se formeze literele unui anumit alfabet ca o succesiune de puncte, liniuțe și spații. Câte litere diferite pot fi formate folosind 5 simboluri?

35. Când se joacă bridge, un pachet de cărți de 52 de foi este distribuit între patru jucători, cu câte 13 cărți pentru fiecare jucător. Câte moduri diferite există de a împărți cărțile?

36. Oficiul poștal vinde cinci tipuri de cărți poștale. Determinați numărul de moduri de a cumpăra șapte cărți poștale.

37. Doi colecționari fac schimb de timbre. Aflați numărul de metode de schimb dacă primul colecționar schimbă 3 timbre, iar al doilea - 6 timbre. (Schimbul are loc pentru o ștampilă).

38. Un elev are 6 cărți de matematică, iar celălalt are 5. În câte moduri pot schimba 2 cărți dintr-una cu 2 cărți ale altuia?

39. Câte permutări diferite de litere pot fi făcute în cuvintele: „blocare”, „rotor”, „defensivă”, „clopot”, „seminar”?

40. În câte moduri diferite pot fi plasate următoarele 9 litere în 9 celule: a, a, a, b, b, b, c, c, c?

41. În mașină sunt 6 locuri. În câte moduri pot intra 6 persoane în această mașină dacă doar doi dintre ei pot ocupa locul șoferului?

42. În câte moduri pot fi extrase 6 cărți care conțin un As și un Rege de aceeași culoare dintr-un pachet de 52 de cărți?

43. Determinați expansiunea pentru n=5.

44. Determinați expansiunea pentru n=8.

45. Găsiți un termen din expansiune care nu conține x (adică care conține x până la puterea zero).

46. ​​​​Găsiți al șaselea termen de expansiune , dacă coeficientul binom al celui de-al treilea termen de la sfârșit este 45.

47. În decădere coeficientul celui de-al treilea termen este cu 44 mai mare decât coeficientul celui de-al doilea termen. Aflați termenul liber, adică termenul de expansiune care nu depinde de x (termenul care nu depinde de x va fi cel care conține x la puterea zero).

48. În expansiunea binomului găsiți termeni care nu conțin iraționalitate.

49. Aflați numărul acelui termen de expansiune , care conține a și b la puteri egale.

Lecția practică nr. 2

(lecție interactivă în grupuri mici)

Funcții booleene

Scopul lecției: să poată construi diverse funcții booleene, să verifice echivalența formulelor booleene (folosind tabelul de adevăr), să determine variabile esențiale și fictive.

Planul lecției:

1. Operații de bază

2. Funcții booleene ale n variabile

3. Echivalențe de bază

Trebuie remarcat faptul că combinatoria este o ramură independentă a matematicii superioare (și nu face parte din terver) și s-au scris manuale grele pe această disciplină, al căror conținut, uneori, nu este mai ușor decât algebra abstractă. Cu toate acestea, o mică parte de cunoștințe teoretice ne va fi suficientă, iar în acest articol voi încerca să analizez într-o formă accesibilă bazele temei cu probleme tipice combinatorii. Și mulți dintre voi mă veți ajuta ;-)

Ce vom face? Într-un sens restrâns, combinatoria este calculul diferitelor combinații care pot fi făcute dintr-o anumită mulțime discret obiecte. Obiectele sunt înțelese ca orice obiecte izolate sau ființe vii - oameni, animale, ciuperci, plante, insecte etc. În același timp, combinatoriei nu îi pasă deloc că setul este format dintr-o farfurie de terci de gris, un fier de lipit și o broască de mlaștină. Este esențial important ca aceste obiecte să poată fi enumerate - sunt trei dintre ele (discretență)și important este că niciuna dintre ele nu este identică.

Ne-am ocupat de multe, acum despre combinații. Cele mai comune tipuri de combinații sunt permutările de obiecte, selecția lor dintr-un set (combinație) și distribuția (plasarea). Să vedem cum se întâmplă asta chiar acum:

Permutări, combinații și plasări fără repetare

Nu vă fie teamă de termeni obscuri, mai ales că unii dintre ei chiar nu sunt foarte buni. Să începem cu coada titlului - ce înseamnă „ fara repetitii"? Aceasta înseamnă că în această secțiune vom lua în considerare seturi care constau din variat obiecte. De exemplu, ... nu, nu o sa ofer terci cu fier de lipit si broasca, mai bine sa ai ceva mai gustos =) Imagineaza-ti ca pe masa din fata ta s-au materializat un mar, o para si o banana ( dacă le aveți, situația poate fi simulată în realitate). Așezăm fructele de la stânga la dreapta în următoarea ordine:

mar / para / banana

Întrebarea unu: În câte moduri pot fi rearanjate?

O combinație a fost deja scrisă mai sus și nu există probleme cu restul:

mar / banana / para
para / mar / banana
pară / banană / măr
banană / măr / peră
banană / peră / măr

Total: 6 combinații sau 6 permutări.

Bine, nu a fost dificil să enumerați toate cazurile posibile, dar dacă există mai multe obiecte? Cu doar patru fructe diferite, numărul de combinații va crește semnificativ!

Vă rugăm să deschideți materialul de referință (este convenabil să tipăriți manualul) iar la punctul nr. 2, găsiți formula pentru numărul de permutări.

Fără bătăi de cap - 3 obiecte pot fi rearanjate în moduri diferite.

Întrebarea doi: În câte moduri poți alege a) un fruct, b) două fructe, c) trei fructe, d) cel puțin un fruct?

De ce alege? Așa că ne-am făcut pofta de mâncare la punctul anterior - pentru a mânca! =)

a) Un fruct poate fi ales, evident, în trei moduri - luați fie un măr, o peră, fie o banană. Calculul formal se efectuează conform formula pentru numărul de combinații:

Intrarea în acest caz trebuie înțeleasă după cum urmează: „în câte moduri poți alege 1 fruct din trei?”

b) Să enumerăm toate combinațiile posibile de două fructe:

măr și pere;
măr și banane;
pere și banane.

Numărul de combinații poate fi verificat cu ușurință folosind aceeași formulă:

Intrarea este înțeleasă într-un mod similar: „în câte moduri poți alege 2 fructe din trei?”

c) Și, în sfârșit, există o singură modalitate de a alege trei fructe:

Apropo, formula pentru numărul de combinații rămâne semnificativă pentru o probă goală:
În acest fel, nu puteți alege niciun fruct - de fapt, nu luați nimic și gata.

d) În câte moduri poți lua cel puțin unul fructe? Condiția „cel puțin unul” implică faptul că suntem mulțumiți cu 1 fruct (oricare) sau cu oricare 2 fructe sau cu toate cele 3 fructe:
folosind aceste metode poți alege cel puțin un fruct.

Cititorii care au studiat cu atenție lecția introductivă despre teoria probabilității, am ghicit deja ceva. Dar mai multe despre semnificația semnului plus mai târziu.

Pentru a răspunde la următoarea întrebare am nevoie de doi voluntari... ...Ei bine, din moment ce nimeni nu vrea, atunci te voi chema la consiliu =)

Întrebarea trei: În câte moduri puteți distribui câte un fruct pentru Dasha și Natasha?

Pentru a distribui două fructe, mai întâi trebuie să le selectați. Conform paragrafului „fi” din întrebarea anterioară, acest lucru se poate face în moduri, le voi rescrie:

măr și pere;
măr și banane;
pere și banane.

Dar acum vor fi de două ori mai multe combinații. Luați în considerare, de exemplu, prima pereche de fructe:
Pe Dasha o poți trata cu un măr și pe Natasha cu o peră;
sau invers - Dasha va primi para, iar Natasha va primi mărul.

Și o astfel de permutare este posibilă pentru fiecare pereche de fructe.

Luați în considerare același grup de studenți care a mers la dans. În câte moduri pot fi împerecheați un băiat și o fată?

În moduri puteți selecta 1 tânăr;
moduri în care poți alege o fată.

Astfel, un tânăr Și Puteți alege o fată: moduri.

Când se selectează 1 obiect din fiecare set, este valabil următorul principiu pentru numărarea combinațiilor: „ fiecare un obiect dintr-un set poate forma o pereche cu fiecare obiect al altui set”.

Adică, Oleg poate invita oricare dintre cele 13 fete la dans, Evgeny poate invita și oricare dintre cele treisprezece, iar restul tinerilor au o alegere similară. Total: posibile perechi.

Trebuie remarcat faptul că, în acest exemplu, „istoria” formării perechii nu contează; totusi, daca tinem cont de initiativa, numarul de combinatii trebuie dublat, intrucat fiecare dintre cele 13 fete poate invita si orice baiat la dans. Totul depinde de condițiile unei anumite sarcini!

Un principiu similar este valabil și pentru combinații mai complexe, de exemplu: în câte moduri poți alege doi tineri? Și două fete să participe la o scenetă KVN?

Uniune ȘI sugerează clar că combinațiile trebuie înmulțite:

Posibile grupuri de artiști.

Cu alte cuvinte, fiecare cu o pereche de băieți (45 de perechi unice) poate performa orice o pereche de fete (78 de perechi unice). Și dacă luăm în considerare distribuția rolurilor între participanți, vor exista și mai multe combinații. ...Îmi doresc foarte mult, dar tot mă voi abține să continui pentru a nu vă insufla o aversiune față de viața de student =).

Regula de înmulțire a combinațiilor se aplică și unui număr mai mare de multiplicatori:

Problema 8

Câte numere din trei cifre sunt divizibile cu 5?

Soluţie: pentru claritate, să notăm acest număr cu trei asteriscuri: ***

ÎN sute de loc Puteți scrie oricare dintre numere (1, 2, 3, 4, 5, 6, 7, 8 sau 9). Zero nu este potrivit, deoarece în acest caz numărul încetează să fie format din trei cifre.

Dar în locul zecilor(„în mijloc”) puteți alege oricare dintre cele 10 cifre: .

Conform condiției, numărul trebuie să fie divizibil cu 5. Un număr este divizibil cu 5 dacă se termină cu 5 sau 0. Astfel, ne mulțumim cu 2 cifre în cifra cea mai puțin semnificativă.

În total, există: numere din trei cifre care sunt divizibile cu 5.

În acest caz, lucrarea este descifrată astfel: „9 moduri în care puteți alege un număr sute de loc Și 10 moduri de a alege un număr în locul zecilor Și 2 moduri de intrare Unități digitale»

Sau chiar mai simplu: „ fiecare de la 9 cifre la sute de loc combine cu fiecare de 10 cifre locul zecilor si cu fiecare de la două cifre la Unități digitale».

Răspuns: 180

Si acum…

Da, aproape că am uitat de comentariul promis la problema nr. 5, în care Bor, Dima și Volodya pot primi câte o carte în moduri diferite. Înmulțirea aici are același sens: modalități de a elimina 3 cărți din pachet ȘI în fiecare eșantion rearanjați-le în moduri.

Și acum o problemă de rezolvat pe cont propriu... acum voi veni cu ceva mai interesant... să fie despre aceeași versiune rusă a blackjack-ului:

Problema 9

Câte combinații câștigătoare de 2 cărți există atunci când joci „punct”?

Pentru cei care nu știu: combinația câștigătoare este 10 + ACE (11 puncte) = 21 de puncte și, să luăm în considerare combinația câștigătoare de doi ași.

(ordinea cărților din orice pereche nu contează)

O scurtă soluție și răspuns la sfârșitul lecției.

Apropo, nu considerați exemplul primitiv. Blackjack-ul este aproape singurul joc pentru care există un algoritm bazat pe matematică care vă permite să învingeți cazinoul. Cei interesați pot găsi cu ușurință o mulțime de informații despre strategia și tacticile optime. Adevărat, astfel de maeștri ajung destul de repede pe lista neagră a tuturor unităților =)

Este timpul să consolidăm materialul acoperit cu câteva sarcini solide:

Problema 10

Vasya are 4 pisici acasă.

a) în câte moduri pot fi așezate pisicile în colțurile camerei?
b) în câte moduri poți lăsa pisicile să iasă la plimbare?
c) în câte moduri poate ridica Vasya două pisici (una în stânga, cealaltă în dreapta)?

Să decidem: în primul rând, ar trebui să acordați din nou atenție faptului că problema se ocupă diferit obiecte (chiar dacă pisicile sunt gemeni identici). Aceasta este o condiție foarte importantă!

a) Tăcerea pisicilor. Sub rezerva acestei executii toate pisicile deodată
+ locația lor este importantă, așa că există permutări aici:
folosind aceste metode poți așeza pisicile în colțurile camerei.

Repet că la permutare contează doar numărul de obiecte diferite și pozițiile lor relative. În funcție de starea de spirit a lui Vasya, ea poate așeza animalele într-un semicerc pe canapea, la rând pe pervaz etc. – în toate cazurile vor exista 24 de permutări Pentru comoditate, cei interesați își pot imagina că pisicile sunt multicolore (de exemplu, alb, negru, roșu și tabby) și să enumere toate combinațiile posibile.

b) În câte moduri poți lăsa pisicile să meargă la plimbare?

Se presupune că pisicile merg la plimbare doar pe ușă, iar întrebarea implică indiferență în ceea ce privește numărul de animale - 1, 2, 3 sau toate cele 4 pisici pot ieși la plimbare.

Numărăm toate combinațiile posibile:

În aceste moduri poți lăsa o pisică (oricare dintre cele patru) să iasă la plimbare;
modalități în care puteți lăsa două pisici să meargă la plimbare (enumerați singur opțiunile);
în moduri poți lăsa trei pisici să iasă la plimbare (una dintre cele patru stă acasă);
Astfel poți elibera toate pisicile.

Probabil ați ghicit că valorile rezultate ar trebui să fie rezumate:
moduri prin care poți lăsa pisicile să meargă la plimbare.

Pentru entuziaști, ofer o versiune complicată a problemei - atunci când orice pisică din orice probă poate ieși aleatoriu afară, atât prin ușă, cât și prin fereastra de la etajul 10. Va fi o creștere vizibilă a combinațiilor!

c) În câte moduri poate Vasya să ridice două pisici?

Situația presupune nu numai alegerea a 2 animale, ci și plasarea lor în fiecare mână:
În aceste moduri puteți ridica 2 pisici.

A doua soluție: puteți alege două pisici folosind metode Și modalități de a planta fiecare un cuplu la indemana:

Răspuns: a) 24, b) 15, c) 12

Ei bine, ca să-ți lamurești conștiința, ceva mai specific despre înmulțirea combinațiilor... Lăsați Vasya să aibă 5 pisici suplimentare =) În câte moduri puteți lăsa 2 pisici să iasă la plimbare? Și 1 pisica?

Adică cu fiecare câteva pisici pot fi eliberate fiecare pisică.

Un alt acordeon cu butoane pentru soluție independentă:

Problema 11

Trei pasageri s-au urcat în liftul unei clădiri cu 12 etaje. Toată lumea, indiferent de ceilalți, poate ieși la orice (începând de la etajul 2) cu aceeași probabilitate. În câte moduri:

1) pasagerii pot coborî la același etaj (Ordinea de ieșire nu contează);
2) două persoane pot coborî la un etaj, iar o a treia la celălalt;
3) oamenii pot ieși pe etaje diferite;
4) pot pasagerii să iasă din lift?

Și aici se întreabă des din nou, clarific: dacă la același etaj ies 2 sau 3 persoane, atunci ordinea de ieșire nu contează. Gândește, folosește formule și reguli pentru a adăuga/înmulți combinații. În caz de dificultăți, este util ca pasagerii să dea nume și să speculeze în ce combinații pot ieși din lift. Nu este nevoie să fii supărat dacă ceva nu merge, de exemplu, punctul nr. 2 este destul de insidios.

Soluție completă cu comentarii detaliate la sfârșitul lecției.

Ultimul paragraf este dedicat combinațiilor care apar destul de des - conform evaluării mele subiective, în aproximativ 20-30% din problemele combinatorii:

Permutări, combinații și plasări cu repetări

Tipurile de combinații enumerate sunt prezentate în paragraful nr. 5 al materialului de referință Formule de bază ale combinatoriei Cu toate acestea, unele dintre ele pot să nu fie foarte clare la prima lectură. În acest caz, este mai întâi recomandabil să vă familiarizați cu exemple practice și abia apoi să înțelegeți formularea generală. Merge:

Permutări cu repetări

În permutările cu repetări, ca în permutările „obișnuite”, toate multele obiecte deodată, dar există un lucru: în această mulțime se repetă unul sau mai multe elemente (obiecte). Îndeplinește următorul standard:

Problema 12

Câte combinații diferite de litere pot fi obținute prin rearanjarea cardurilor cu următoarele litere: K, O, L, O, K, O, L, b, Ch, I, K?

Soluţie: în cazul în care toate literele ar fi diferite, atunci ar trebui aplicată o formulă banală, dar este complet clar că pentru setul de cărți propus unele manipulări vor funcționa „inactiv”, de exemplu, dacă schimbați oricare două cărți cu literele „K” „ în orice cuvânt, obțineți același cuvânt. Mai mult, fizic cărțile pot fi foarte diferite: una poate fi rotundă cu litera „K” imprimată pe ea, cealaltă poate fi pătrată cu litera „K” desenată pe ea. Dar, în funcție de sensul sarcinii, chiar și astfel de cărți sunt considerate la fel, deoarece condiția întreabă despre combinațiile de litere.

Totul este extrem de simplu - doar 11 cărți, inclusiv litera:

K – repetat de 3 ori;
O – repetat de 3 ori;
L – repetat de 2 ori;
b – repetat 1 dată;
H – repetat 1 dată;
Și - repetat 1 dată.

Verificați: 3 + 3 + 2 + 1 + 1 + 1 = 11, ceea ce trebuia verificat.

Conform formulei numărul de permutări cu repetări:
pot fi obținute diferite combinații de litere. Mai mult de jumătate de milion!

Pentru a calcula rapid o valoare factorială mare, este convenabil să utilizați funcția standard Excel: introduceți în orice celulă =FACT (11)și apăsați introduce.

În practică, este destul de acceptabil să nu scrieți formula generală și, în plus, să omiteți factorii unitari:

Dar sunt necesare comentarii preliminare despre scrisorile repetate!

Răspuns: 554400

Un alt exemplu tipic de permutări cu repetare apare în problema de plasare a pieselor de șah, care poate fi găsită în depozit. soluții gata făcuteîn pdf-ul corespunzător. Și pentru o soluție independentă, am venit cu o sarcină mai puțin formulă:

Problema 13

Alexey face sport și 4 zile pe săptămână - atletism, 2 zile - exerciții de forță și 1 zi de odihnă. În câte moduri își poate crea un program săptămânal?

Formula nu funcționează aici, deoarece ia în considerare schimburile întâmplătoare (de exemplu, schimbarea exercițiilor de forță de miercuri cu exercițiile de forță de joi). Și din nou - de fapt, aceleași 2 sesiuni de antrenament de forță pot fi foarte diferite unele de altele, dar în contextul sarcinii (din punct de vedere al programului) sunt considerate aceleași elemente.

Soluție pe două rânduri și răspuns la sfârșitul lecției.

Combinații cu repetări

O trăsătură caracteristică a acestui tip de combinație este că eșantionul este extras din mai multe grupuri, fiecare dintre ele constând din obiecte identice.

Toată lumea a muncit din greu astăzi, așa că este timpul să vă împrospătați:

Problema 14

Cantina studențească vinde cârnați în aluat, cheesecake și gogoși. În câte moduri puteți cumpăra cinci plăcinte?

Soluţie: acordați atenție imediată criteriului tipic pentru combinații cu repetări - în funcție de condiție, nu este un set de obiecte ca atare oferit la alegere, ci tipuri diferite obiecte; se presupune că sunt la vânzare cel puțin cinci hot dog, 5 cheesecake și 5 gogoși. Plăcintele din fiecare grupă sunt, desigur, diferite - pentru că gogoșile absolut identice pot fi simulate doar pe computer =) Cu toate acestea, caracteristicile fizice ale plăcintelor nu sunt semnificative în scopul problemei, iar hot-dog-urile / cheesecake-urile / gogoșile din grupurile lor sunt considerate la fel.

Ce ar putea fi în eșantion? În primul rând, trebuie menționat că cu siguranță vor exista plăcinte identice în probă (deoarece alegem 5 bucăți și există 3 tipuri din care să alegeți). Există opțiuni aici pentru toate gusturile: 5 hot dog, 5 cheesecake, 5 gogoși, 3 hot dog + 2 cheesecake, 1 hot dog + 2 cheesecake + 2 gogoși etc.

Ca și în cazul combinațiilor „obișnuite”, ordinea selecției și plasarea plăcintelor în selecție nu contează - ați ales doar 5 bucăți și atât.

Folosim formula numărul de combinații cu repetări:
Puteți cumpăra 5 plăcinte folosind această metodă.

Poftă bună!

Răspuns: 21

Ce concluzie se poate trage din multe probleme combinatorii?

Uneori, cel mai greu este să înțelegeți starea.

Un exemplu similar pentru o soluție independentă:

Problema 15

Portofelul conține un număr destul de mare de monede de 1, 2, 5 și 10 ruble. În câte moduri pot fi scoase trei monede dintr-un portofel?

În scopuri de autocontrol, răspunde la câteva întrebări simple:

1) Toate monedele din eșantion pot fi diferite?
2) Numiți combinația de monede „cea mai ieftină” și cea mai „scumpe”.

Soluție și răspunsuri la sfârșitul lecției.

Din experiența mea personală, pot spune că combinațiile cu repetiții sunt cel mai rar invitat în practică, ceea ce nu se poate spune despre următoarele tipuri de combinații:

Plasări cu repetări

Dintr-un set format din elemente, elementele sunt selectate, iar ordinea elementelor în fiecare selecție este importantă. Și totul ar fi bine, dar o glumă destul de neașteptată este că putem selecta orice obiect din setul original de câte ori vrem. Figurat vorbind, „mulțimea nu va scădea”.

Când se întâmplă asta? Un exemplu tipic este un lacăt cu combinație cu mai multe discuri, dar din cauza dezvoltărilor tehnologice, este mai relevant să luăm în considerare descendentul său digital:

Problema 16

Câte coduri PIN din patru cifre există?

Soluţie: de fapt, pentru a rezolva problema, cunoașterea regulilor combinatoriei este suficientă: în moduri puteți selecta prima cifră a codului PIN Și moduri - a doua cifră a codului PIN Șiîn tot atâtea feluri – al treilea Și același număr - al patrulea. Astfel, conform regulii înmulțirii combinațiilor, un cod pin de patru cifre poate fi compus în: moduri.

Și acum folosind formula. Conform condiției, ni se oferă un set de numere, din care numerele sunt selectate și aranjate într-o anumită ordine, în timp ce numerele din eșantion pot fi repetate (adică orice cifră a setului original poate fi folosită de un număr arbitrar de ori). Conform formulei pentru numărul de plasări cu repetări:

Răspuns: 10000

Ce îmi vine în minte aici... ...dacă ATM-ul „mâncă” cardul după a treia încercare nereușită de a introduce codul PIN, atunci șansele de a-l ridica la întâmplare sunt foarte mici.

Și cine a spus că combinatoria nu are sens practic? Sarcină cognitivă pentru toți cititorii site-ului:

Problema 17

Conform standardului de stat, o plăcuță de înmatriculare a mașinii este formată din 3 numere și 3 litere. În acest caz, un număr cu trei zerouri este inacceptabil, iar literele sunt selectate din setul A, B, E, K, M, N, O, P, S, T, U, X (se folosesc doar acele litere chirilice a căror ortografie coincide cu literele latine).

Câte plăcuțe de înmatriculare diferite pot fi create pentru o regiune?

Nu atât de mulți dintre ei, apropo. În regiunile mari nu există suficientă o astfel de cantitate și, prin urmare, pentru ei există mai multe coduri pentru inscripția RUS.

Soluția și răspunsul sunt la sfârșitul lecției. Nu uitați să folosiți regulile combinatoriei ;-) ...Am vrut să arăt ceea ce era exclusiv, dar s-a dovedit că nu este exclusiv =) M-am uitat pe Wikipedia - acolo sunt calcule, deși fără comentarii. Deși în scop educațional, probabil, puțini oameni au rezolvat-o.

Lecția noastră incitantă s-a încheiat și, în sfârșit, vreau să spun că nu ți-ai pierdut timpul - pentru că formulele combinatorice își găsesc o altă aplicație practică vitală: se găsesc în diverse probleme în teoria probabilității,
si in probleme care implică determinarea clasică a probabilităţii– mai ales des =)

Vă mulțumim tuturor pentru participarea activă și ne vedem curând!

Soluții și răspunsuri:

Sarcina 2: Soluţie: găsiți numărul tuturor permutărilor posibile a 4 cărți:

Când un card cu zero este plasat pe primul loc, numărul devine din trei cifre, așa că aceste combinații ar trebui excluse. Fie zero pe primul loc, apoi celelalte 3 cifre din cifrele inferioare pot fi rearanjate în moduri diferite.

Notă : deoarece Deoarece există doar câteva cărți, este ușor să enumerați toate opțiunile aici:
0579
0597
0759
0795
0957
0975

Astfel, din setul propus putem realiza:
24 – 6 = 18 numere din patru cifre
Răspuns : 18

Sarcina 4: Soluţie: în moduri puteți alege 3 cărți din 36.
Răspuns : 7140

Sarcina 6: Soluţie: moduri.
O alta solutie : moduri prin care puteți selecta două persoane din grup și și
2) Setul „cel mai ieftin” conține 3 monede de ruble, iar cel mai „scump” – 3 monede de zece ruble.

Problema 17: Soluţie: folosind aceste metode, puteți crea o combinație digitală a unui număr de mașină, în timp ce unul dintre ele (000) ar trebui exclus: .
folosind aceste metode puteți crea o combinație de litere a unui număr de înmatriculare.
Conform regulii înmulțirii combinațiilor, totalul se poate face:
plăcuțe de înmatriculare
(fiecare combinația digitală este combinată cu fiecare combinație de litere).
Răspuns : 1726272