Mely kombinációknál fontos az elemek sorrendje? Kombinatorikai képletek

Feladat . Határozza meg az összes rendezett készlet számát hossz r, amely a halmaz elemeiből állhat össze x (
), ha az egyes elemek kiválasztása
, a teljes készletből készül x.

Rendelt készlet
a karteziánus szorzat eleme
, a következőket tartalmazza r azonos szorzók x. A szorzatszabály szerint egy halmaz elemeinek száma
egyenlő
. Levezettük a képletet
.

Példa. Hány négyjegyű telefonszám készíthető mind a tíz számjegyből?

Itt
, a telefonszámok száma pedig

2.1.5. Elhelyezések ismétlés nélkül

Feladat . Hány megrendelt készlet
-ből lehet összeállítani n a készlet elemei x, ha a halmaz minden eleme eltérő?

Első elem választhat n módokon. Ha az első elem már ki van jelölve, akkor a második elem csak választani lehet
módokon, és ha már kiválasztották
elem
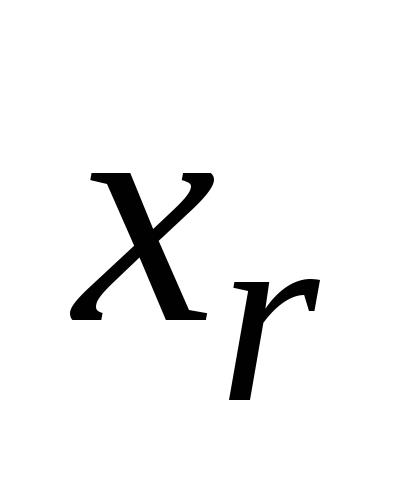, majd az elemet választhat
módokon (már kiválasztott elem ismétlése nem megengedett). A termékszabály szerint kapjuk

Ezt a képletet másképp írjuk le a jelöléssel
. Mert

.

Példa. Hány különböző listája lehet az olimpia győzteseinek (első, második, harmadik helyezett), ha 20-an vettek részt? Emberi?

Itt
, a szükséges szám

2.1.6. Permutációk ismétlés nélkül

Tekintsük az ismétlés nélküli elhelyezés speciális esetét: ha
, akkor a halmaz összes eleme részt vesz az elhelyezésben x, azaz a minták azonos összetételűek és csak az elemek sorrendjében térnek el egymástól. Az ilyen mintákat ún permutációk . Permutációk száma innen n elemek képviselik :

Példa. Hányféleképpen lehet sorba állni a pénztárnál, ha hat ember akar fizetést kapni?

2.1.7. Permutációk ismétlésekkel

Hagyja a készletet x tartalmazza k különféle elemek:
.Permutáció ismétlésekkel fogalmazás
megrendelt hosszkészletet fogunk hívni
, amelyben az elem találkozik egyszer
. Az ilyen permutációk számát jelöljük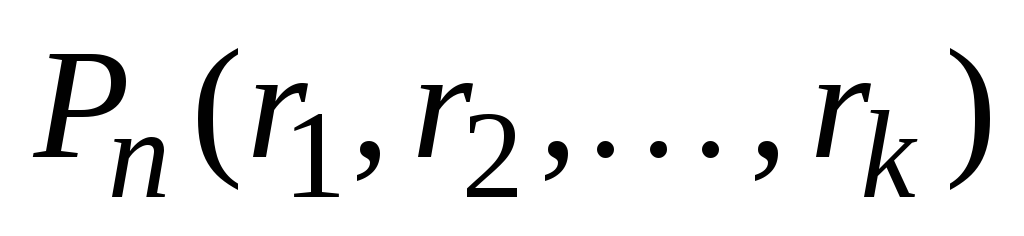
.

Példa. A levelekből
írjunk egy permutációt a kompozíció ismétlésével
. A hossza
, és a levél a 2-szer lép be, b- 2 alkalommal, c-egyszer. Ilyen permutáció lehet pl.
vagy
.

Vezessük le az ismétlések permutációinak számának képletét. Számozzuk meg a permutációban szereplő összes azonos elemet különböző indexekkel, pl. átrendezés helyett
kapunk
. Most a permutáció minden eleme különbözik, és az ilyen permutációk száma egyenlő
. Az első elem megjelenik a kijelölésben egyszer. Távolítsuk el az indexeket az első elemből (példánkban a permutációt kapjuk
), míg a különböző permutációk száma -kal csökken alkalommal, mert ha megváltoztatjuk az azonos elemek sorrendjét, a mintánk nem változik. Ha a második elemből eltávolítjuk az indexeket, akkor a permutációk száma eggyel csökken egyszer. És így tovább, egészen a számmal rendelkező elemig k– a permutációk száma eggyel csökken egyszer. Megkapjuk a képletet

Példa. Hány különböző „szót” kaphat az „átvitel” szó betűinek átrendezésével?

Ebben a szóban az „e” és „a” betű kétszer, a többi egyszer szerepel. A kompozíció ismétlésével járó átrendeződésről beszélünk
hossz. Az ilyen permutációk száma egyenlő

2.1.8. Kombinációk

Feladat . Hány különböző készlet r elemeket tartalmazó halmazból összeállíthatók n elemek?

Először a megrendelt készleteket állítjuk össze r elemek mindegyikében. Az ilyen készletek száma (ezek elhelyezések innen: n elemek által r) egyenlő
. Most figyelembe vesszük, hogy az elemek írási sorrendje számunkra nem számít. Ugyanakkor től különböző elhelyezések, amelyek csak az elemek sorrendjében térnek el egymástól, egy kombinációt kapunk. Például két különböző elhelyez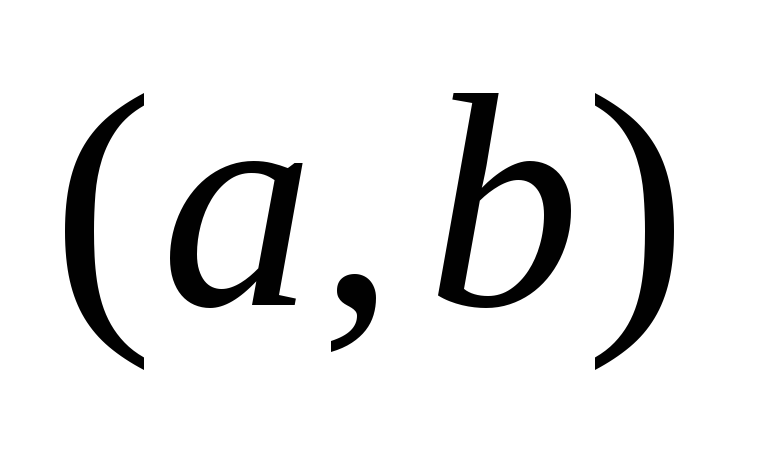és
És
két elem egy kombinációnak felel meg
. Így a kombinációk száma V alkalommal kevesebb, mint az elhelyezések száma :

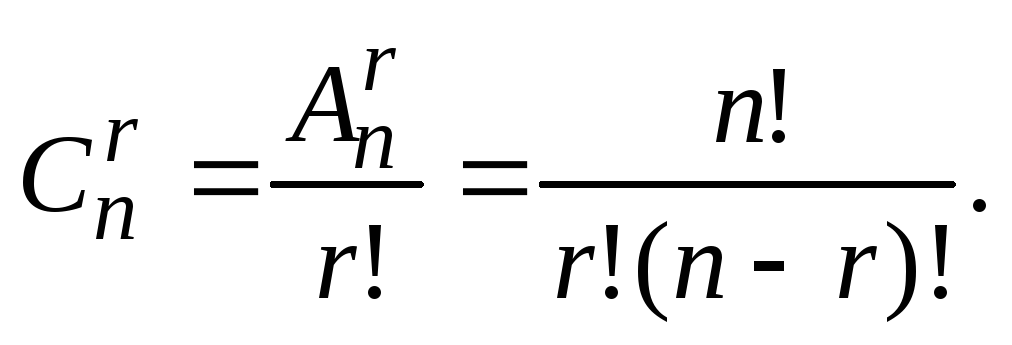
Példa. A nyolc ablaktörlő közül hány módon választhatunk hármat

A permutáció a következő elemek kombinációja N különböző elemek meghatározott sorrendben. Az átrendezésnél fontos az elemek sorrendje, az átrendezésbe minden elemet be kell vonni. N elemeket.

Feladat: Keresse meg az 1, 2, 3 számsorozat összes lehetséges permutációját!
A következő permutációk léteznek:

1: 1 2 3
2: 1 3 2
3: 2 1 3
4: 2 3 1
5: 3 1 2
6: 3 2 1

Permutációk ismétlés nélkül

A permutációk száma N különböző elemre N!. Igazán:

• Ezek közül bármelyik helyezhető az első helyre N elemek (összes lehetőség N),
• a fennmaradók bármelyike ​​a második pozícióba helyezhető (N-1) elemek (összes lehetőség N·(N-1)),
• ha folytatjuk ezt a sorozatot mindenkinek N helyeken kapjuk: N·(N-1)·(N-2)· … ·1, vagyis összesen N! permutációk.

Tekintsük a számok összes permutációjának megszerzésének problémáját 1…N(vagyis hosszúságú sorozatok N), ahol minden szám pontosan 1-szer jelenik meg. Számos lehetőség van a permutációk beszerzésének sorrendjére. A leggyakrabban megoldott probléma azonban a permutációk generálása lexikográfiai sorrendben (lásd a fenti példát). Ebben az esetben az összes permutációt először az első szám szerint rendezi, majd a második szám szerint stb. növekvő sorrendben. Tehát az első a permutáció lesz 1 2…N, és az utolsó - N N-1…1.

Nézzünk egy algoritmust a probléma megoldására. Meg van adva az eredeti számsor. Minden további permutáció eléréséhez a következő lépéseket kell végrehajtania:

• Végig kell nézni az aktuális permutációt jobbról balra, és egyúttal meg kell győződni arról, hogy a permutáció minden további eleme (a nagyobb számú elem) nem több, mint az előző (a kisebb számú elem) . Amint ez az arány megsérül, meg kell állnia, és meg kell jelölnie az aktuális számot (1. pozíció).
• Tekintse át újra a megtett utat jobbról balra, amíg el nem érjük az első számot, amely nagyobb, mint az előző lépésben jelölt.
• Cserélje fel a kapott két elemet.
• Most a tömb azon részében, amely az 1. pozíciótól jobbra található, az összes számot növekvő sorrendbe kell rendeznie. Mivel ezt megelőzően mindegyiket már csökkenő sorrendben írták, egyszerűen meg kell fordítani az utósor ezen részét.

Így egy új sorozatot kapunk, amelyet a következő lépésben kezdeti sorozatnak tekintünk.

Megvalósítás C++ nyelven

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

#beleértve
névtér használata std;

{
int s = a[i];
a[i] = a[j];
a[j] = s;
}
bool NextSet(int *a, int n)
{
int j = n-2;
while (j != -1 && a[j] >= a) j--;
ha (j == -1)
return false; // nincs több permutáció
int k = n-1;
míg (a[j] >= a[k]) k--;
csere(a, j, k);
int l = j + 1, r = n - 1;
míg (l csere(a, l++, r--);
return true;
}
void Print(int *a, int n) // a permutáció kimenete
{
statikus int szám = 1; // permutációs szám
cout.width(3);
cout<< num++ << ": " ;
for (int i = 0; i< n; i++)
cout<< a[i] << " " ;
cout<< endl;
}
int main()
{
int n, *a;
cout<< "N = " ;
cin >> n;
a = új int [n];
for (int i = 0; i< n; i++)
a[i] = i + 1;
Print(a, n);
while (NextSet(a, n))
Print(a, n);
cin.get(); cin.get();
visszatérés 0;
}

A végrehajtás eredménye

Permutációk ismétlésekkel

Külön figyelmet érdemel a permutációk generálásának problémája N elemeket, ha a sorozat elemei megismételhetők. Tegyük fel, hogy az eredeti sorozat elemekből áll n 1 , n 2 ... n k, ahol elem n 1 ismétli önmagát r 1 egyszer, n 2 ismétli önmagát r 2 idők stb. Ahol n 1 +n 2 +...+n k =N. Ha mindent beleszámolunk n 1 +n 2 +...+n k egy permutáció különböző ismétlődésű elemei, akkor összesen a permutációk különböző változatai vannak ( n 1 +n 2 +...+n k)!. E permutációk között azonban nem mindegyik különbözik egymástól. Valójában mindent r 1 elemeket n 1 helyet cserélhetünk egymással, és ez nem változtat a permutáción. Ugyanígy átrendezhetjük az elemeket n 2, n 3 stb Ennek eredményeként van r 1! lehetőségek ugyanazon permutáció írására az ismétlődő elemek különböző elrendezésével n 1. Így bármilyen permutáció írható r 1 !·r 2 !·...·r k ! módokon. Ezért a különböző permutációk száma ismétlődésekkel egyenlő

Az ismétlésekkel járó permutációk generálásához használhatja a fent megadott, ismétlés nélküli permutációkat generáló algoritmust. Vezessünk be egy ismétlődő elemet az a tömbbe. Alább látható a programkód az ismétlésekkel történő permutációk generálásához (csak a main() függvénykód módosul).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

#beleértve
névtér használata std;
void swap(int *a, int i, int j)
{
int s = a[i];
a[i] = a[j];
a[j] = s;
}
bool NextSet(int *a, int n)
{
int j = n-2;
while (j != -1 && a[j] >= a) j--;
ha (j == -1)
return false; // nincs több permutáció
int k = n-1;
míg (a[j] >= a[k]) k--;
csere(a, j, k);
int l = j + 1, r = n - 1; // rendezi a sorozat többi részét
míg (l csere(a, l++, r--);
return true;
}
void Print(int *a, int n) // a permutáció kimenete
{
statikus int szám = 1; // permutációs szám
cout.width(3); // a permutációs szám kimeneti mezőjének szélessége
cout<< num++ << ": " ;
for (int i = 0; i< n; i++)
cout<< a[i] << " " ;
cout<< endl;
}
int main()
{
int n, *a;
cout<< "N = " ;
cin >> n;
a = új int [n];
for (int i = 0; i< n; i++)
a[i] = i + 1;
a = 1; // ismétlődő elem
Print(a, n);
while (NextSet(a, n))
Print(a, n);
cin.get(); cin.get();
visszatérés 0;
}

A fenti algoritmus eredménye:

Terv:

1. A kombinatorika elemei.

2. A kombinatorika általános szabályai.

4. Gráfok (sémák) alkalmazása kombinatorikai feladatok megoldásában.

Kombinatorika A matematika egy olyan területe, amelyben azt a kérdést vizsgálják, hogy egy adott halmazhoz tartozó elemekből bizonyos feltételek mellett hány különböző kombináció készíthető.

A kombinatorika a 16. században keletkezett. A szerencsejáték (kártya, kocka) akkoriban nagy helyet foglalt el a társadalom kiváltságos rétegeinek életében. Széles körben elterjedtek a lottójátékok. Kezdetben a kombinatorikus problémák elsősorban a szerencsejátékot érintették: hányféleképpen lehet egy adott számú pontot szerezni 2 vagy 3 dobókocka dobásával, vagy hányféleképpen lehet 2 királyt szerezni egy adott kártyajátékban. Ezek és a szerencsejáték egyéb problémái voltak a hajtóereje a kombinatorika, majd a valószínűségszámítás fejlődésének.

Tartaglia olasz matematikus volt az egyik első, aki megszámolta a különböző kombinációk számát kockajáték közben. Összeállította a táblázatokat (az r kockán k pontszerzési módok száma). Azt azonban nem vette figyelembe, hogy ugyanannyi pont különböző módon eshet, így táblázatai nagyszámú hibát tartalmaztak.

A kombinatorikai kérdések elméleti tanulmányozására a 17. században Blaise Pascal és Fermat francia matematikusok vállalkoztak. Kutatásuk kiindulópontja szintén a szerencsejáték-problémák volt.

A kombinatorika további fejlődése J. Bernoulli, G. Leibniz, L. Euler nevéhez fűződik. Munkájukban azonban főszerepet játszottak a különféle játékokra való alkalmazások.

Manapság a kombinatorikus módszereket alkalmazzák a szállítási problémák megoldására, különösen az ütemezési problémákra, a termelési tervek és a termékek értékesítésére stb.

Összeg szabály: Ha egy A objektumot m, egy B objektumot k módon lehet kiválasztani, akkor az „A vagy B” objektumot m + k módon lehet kiválasztani.

Példák:

1. Tegyük fel, hogy egy dobozban n különböző színű golyó van. 1 golyó véletlenszerűen kerül ki. Hányféleképpen lehet ezt megtenni?

Válasz: n módon.

Osszuk el ezt az n golyót két dobozba: az elsőben m, a másodikban k golyó van. Egy véletlenszerűen kiválasztott dobozból véletlenszerűen 1 golyó kerül kihúzásra. Hányféleképpen lehet ezt megtenni?

Megoldás: A labda az első dobozból m, a másodikból pedig k módon távolítható el. Ekkor az összes utak száma m+k=n.

A tengeri szemaforban az ábécé minden betűje két zászló bizonyos helyzetének felel meg a jeladó testéhez képest. Hány ilyen jel lehet?

Megoldás: A teljes szám azoknak a pozícióknak az összege, amikor mindkét zászló a jeladó testének ellentétes oldalán található, és azoknak a pozícióknak az összege, amelyek a jeladó testének ugyanazon oldalán helyezkednek el. A lehetséges pozíciók számának számításakor az összegzési szabály érvényesül.

Termékszabály: Ha az A objektum m módon választható ki, és minden ilyen választás után egy másik B objektum választható ki (függetlenül az A objektum kiválasztásától) k módon, akkor az „A és B” objektumpárok m * k szerint választhatók ki. módokon.

Példák:

Megoldás: A tízesek száma tetszőleges számmal jelölhető 1-től 9-ig. Az egyesek száma 0-tól 9-ig tetszőleges számmal jelölhető. Ha a tízesek száma 1, akkor az egyesek száma tetszőleges szám lehet (0-tól). 9-ig). Így 10 kétjegyű szám van, amelyekben a tízesek száma 1. Hasonlóan gondolkodunk minden más tízes szám esetén is. Akkor kiszámolhatjuk, hogy 9 van *10 = 90 kétjegyű szám.

2. 2 fiók található. Az egyikben m sokszínű kocka, a másikban pedig k többszínű golyó található. Hányféleképpen választhatod ki a „kocka-labda” párost?

Megoldás: A labda kiválasztása nem a kockaválasztástól függ, és fordítva. Ezért egy adott pár kiválasztási módjainak száma m *k .

Népesség ismétlődések nélkül véges számú különböző elem halmaza: a 1, a 2, a 3, ..., a n.

Példa: n halmaza sokszínű reszelék.

Mintavételi térfogatk (kn) egy adott sokaság m elemének csoportja.

Példa: A megadott n közül kiválasztott m sokszínű törmelékből varrt tarka szalag.

Bejegyzések innenn elem egyenkéntk ilyen mintáknak nevezzük azokat, amelyek egyenként k elemet tartalmaznak, az általános sokaság adott n eleme közül ismétlés nélkül kiválasztva, és akár az elemek összetételében, akár elrendezésük sorrendjében különböznek egymástól.

- elhelyezések száma től n által k.

Elhelyezések száma innen n által k a következő módon határozható meg: az első kiválasztási objektum kiválasztható n módokon, akkor a második objektum kiválasztható n -1 út stb.

Ezt a képletet átalakítva a következőket kapjuk:

Emlékeztetni kell arra 0!=1.

Példák:

1. A labdarúgó bajnokság A osztályának első csoportjában 17 csapat vesz részt. Érmeket osztanak ki: arany, ezüst és bronz. Hányféleképpen lehet őket játszani?

Megoldás:A nyertes csapatkombinációk az elemek összetételében és sorrendjében különböznek egymástól, pl. 17 és 3 között helyezkednek el.

2. A tudományos társaság 25 főből áll. Meg kell választani az egyesület elnökét, alelnökét, tudományos titkárát és pénztárosát. Hányféleképpen lehet ezt megtenni?

Megoldás: A cégvezetés kombinációi az elemek összetételében és sorrendjében különböznek egymástól, pl. 25 és 4 között helyezkednek el.

Permutációk ismétlődés nélkül innen nelemeketaz ismétlődés nélküli elhelyezéseknek nevezzük n eleme n , azaz az elhelyezések csak az elemek sorrendjében térnek el egymástól.

Permutációk száma.

Példák:

1. Hány különböző ötjegyű szám készíthető az 1, 2, 3, 4, 5 számjegyekből, feltéve, hogy különböző számjegyekből kell állniuk?

Ismétlések nélküli kombinációk től nelemek általk ilyen mintáknak nevezzük azokat, amelyek egyenként k elemet tartalmaznak, az általános sokaság adott n eleme közül választva ismétlés nélkül, és csak az elemek összetételében térnek el egymástól.

- kombinációinak száma n által k

1. Ha egy sakkbajnokság elődöntőjében 20-an vesznek részt, és csak hárman jutnak a döntőbe, akkor ez a három hányféleképpen határozható meg?

Megoldás:Ebben az esetben ennek a hármasnak a sorrendje nem jelentős. Ezért a döntőbe jutott hármasok 20:3 kombinációi.

Megoldás:Ebben az esetben ennek a hármasnak a sorrendje nem jelentős. Ezért a delegált hármasok 10:3 kombinációi.

Absztrakt:

4.Gáfok (sémák) használata kombinatorikus feladatok megoldásában.

Abban az esetben, ha az egyes lépésekben a lehetséges választási lehetőségek száma attól függ, hogy mely elemeket választották ki korábban, a kombinációk összeállításának folyamata „faként” ábrázolható. Először is, annyi szegmens rajzolódik ki egy pontból, ahány különböző választási lehetőség van az első lépésben. Minden szegmens végéről rajzoljon annyi szegmenst, amennyi a második lépésben kiválasztható, ha az első lépésben ez az elem lett kiválasztva stb.

Feladat:

Az űrhajó parancsainak összeállításakor figyelembe veszik az utazás résztvevőinek pszichológiai kompatibilitásának kérdését is. Az űrhajó legénységét 3 főből kell összeállítani: egy parancsnok, egy mérnök és egy orvos. A parancsnoki posztra 4 jelölt van: a 1, a 2, a 3, a 4 .A 3. mérnök helyére:b 1, b 2, b 3. Orvosi helyért - 3: c 1, c 2, c 3. Az ellenőrzés kimutatta, hogy a parancsnokAz a 1 pszichológiailag kompatibilis a b 1 és b 3 mérnökökkelés c 1 és c 3 orvosok. Parancsnok egy 2 - mérnökökkel b 1 és b 2 . és az összes orvos. Parancsnoka 3 - mérnökökkelb 1 és b 2és az orvosokc 1 és c 3. Parancsnok a 4 - az összes mérnökkel és az orvossal c 2. Ezen kívül mérnökb 1 nem kompatibilis az orvossal c 3, b 2 - orvossal c 1 és b 3 - orvossal c 2. Hányféleképpen állítható össze a hajó legénysége ilyen körülmények között?

Megoldás:

Hozzuk létre a megfelelő „fát”.

Válasz: 10 kombináció.

Egy ilyen fa egy gráf, és kombinatorikus problémák megoldására szolgál.

Az óra célja: legyen képes alapvető kombinatorikai képletek alkalmazására és ismerje e képletek alkalmazásának feltételeit; ismeri a binomiális együtthatók tulajdonságait, és meg tudja határozni a binomiális kiterjesztését n adott értékére.

Tanterv:

1. Elhelyezések száma.

2. Permutációk száma.

3. Kombinációk száma.

4. Ismétlések.

5. Newton-binomiális. Pascal-háromszög.

Útmutató a téma tanulmányozásához

Sok gyakorlati esetben szükségessé válik az objektumok lehetséges kombinációinak számbavétele, amelyek bizonyos feltételeket kielégítenek. Az ilyen problémákat kombinatorikusnak nevezzük. A kombinatorikai problémák sokfélesége nem írható le kimerítően, de közöttük számos különösen elterjedt, számítási módszer ismert.

Kombinatorika- a matematika olyan területe, amelyben azt a kérdést vizsgálják, hogy egy adott halmazhoz tartozó elemekből bizonyos feltételek mellett hány különböző kombináció készíthető. A „kombinatorika” kifejezés a latin combina szóból származik – egyesíteni, összekapcsolni.

Legyen egy n elemű halmaz: x 1, x 2, x 3, ..., x n.

Ebből a halmazból különböző részhalmazokat, azaz mintákat képezhetünk, amelyek mindegyike m elemet tartalmaz (0 ≤ m ≤ n). Vannak rendezett kijelölések (elhelyezések), permutációk és rendezetlen kijelölések (kombinációk).

Elhelyezések

Elhelyezések n szerint különféle elemek m olyan elemek, amelyek akár az elemek összetételében, akár sorrendjükben különböznek egymástól.

Elhelyezések száma innen n elemek által m elemeket jelölnek ki (A a francia szó elrendezésének első betűje, ami elhelyezést, rendbetételt jelent), és a következő képlettel számítják ki:

A faktoriális fogalma

Munka n természetes számok 1-től n szimbólum jelzi n! (n faktoriális), azaz

Például 2!=

5!=

Megjegyzendő, hogy célszerű 0!-t kiszámítani, ha definíció szerint 0!=1.

Példák:

Az utolsó két képletből az következik

Példa.

8 csapat vesz részt egy egyfordulós labdarúgó tornán. Hány lehetőség van az első háromba?

Megoldás: Mivel fontos a csapatok sorrendje az első háromban, ezért helyezésekkel foglalkozunk. Akkor

(lehetőségek).

Példa.

Hányféleképpen lehet kiválasztani három személyt tíz jelölt közül három különböző pozícióra?

Megoldás:

(módokon).

Példa.

Hány telefonszám állhat 5 számjegyből úgy, hogy minden egyes számban minden számjegy más legyen?

(telefonszámok).

Átrendezések

Permutációk ugyanazokból álló kombinációk n különböző elemek és csak elrendezésük sorrendjében különböznek egymástól.

Az n elem összes lehetséges permutációjának számát P n jelöli (P a francia permutation szó első betűje, ami permutációt jelent), és a következő képlettel számítjuk ki:

Példa.

A 100 méteres döntőben 8 versenyző indul. Hány versenyprotokoll-lehetőség van?

Megoldás:

Ebben az esetben 8 elem összes permutációjáról beszélünk. Ezután (opciók)

Példa.

Hányféleképpen ülhet 10 ember egy padon?

Megoldás:

(módokon)

Példa.

Hányféleképpen lehet 7 embert leültetni egy asztalhoz 7 evőeszközzel?

Megoldás:

(módokon).

Kombinációk

Kombinációk kombinációk készültek n szerint különféle elemek m olyan elemek, amelyek legalább egy elemben különböznek egymástól.

A kombinációk számát a következő képlet segítségével számítjuk ki: (C a francia szókombináció első betűje).

Példa.

Hányféleképpen lehet tíz jelölt közül három személyt kiválasztani három azonos pozícióra?

Megoldás:

(módokon).

Példa.

Hányféleképpen választhat ki három részt egy 15 alkatrészt tartalmazó dobozból?

Megoldás:

(módokon).

Egy másik típusú képlet az elhelyezések számához és a kombinációk számához

; , vagyis .

A kombinációk számának tulajdonságai:

5)

A kombinatorikai feladatok megoldása során a következő szabályokat kell alkalmazni:

Összeg szabály. Ha egy A objektum n módon választható ki objektumok halmazából, egy másik B objektum pedig k módon, akkor az „A vagy B” objektum n + k módon választható ki.

Termékszabály. Ha egy bizonyos A objektum n módon választható ki egy objektumhalmazból, és minden ilyen kijelölés után egy másik B objektum k módon, akkor egy objektumpár (A, B) a megadott sorrendben n × k módon választható ki. .

Ha néhány elem megismétlődik, akkor ebben az esetben az ismétlődő kombinációkat más képletekkel számítják ki.

Elhelyezések ismétlésekkel

Elhelyezések száma szerint m elemekből származó ismétlődésekkel n a különböző elemek egyenlőek n m, vagyis

Példa.

Az 1,2,3,4,5 számokból 5 3 = 125 háromjegyű számot készíthetünk, ha ugyanabban a számban ugyanazok a számok szerepelhetnek.

Permutációk ismétlésekkel

Ha között n vannak elemek n 1 azonos típusú elemek, n 2 más típusú elemek stb., akkor az ismétlődésekkel járó permutációk száma

Ahol

Példa.

Hány különböző betűváltoztatás végezhető a „matematika” szóban?

Megoldás:

Kombinációk ismétlésekkel

A kombinációk száma ismétlésekkel től n szerint különféle elemek m elemek száma megegyezik a kombinációk számával a következőtől: n+m-1) különböző elemek szerint m elemek:

Példa.

Határozza meg a kombinációk számát négy elem ismétlésével a, b, c, d 3 elem egyenként.

Megoldás:

A szükséges szám lesz

Binomiális tétel

Egy tetszőleges n pozitív egész számra a következő képlet érvényes:

Ez Newton binomiálisa. Az együtthatókat binomiális együtthatóknak nevezzük.

n = 2 esetén megkapjuk a képletet;

n = 3 esetén megkapjuk a képletet.

Példa. Határozza meg a kiterjesztést n=4 esetén.

Megoldás:

A binomiális együtthatók számos tulajdonsággal rendelkeznek:

2. ;

Tekintsük a következő háromszöget:

………………………….

Az n sorszámú sor binomiális tágulási együtthatókat tartalmaz. Az ingatlan kihasználása , észreveheti, hogy a háromszög minden belső eleme egyenlő a felette lévő két elem összegével, a háromszög oldalsó elemei pedig egységekkel egyenlők:

……………………….

Ez Pascal háromszöge. Lehetővé teszi a binomiális együtthatók értékeinek gyors megtalálását.

Az orosz nyelvű irodalomban azokat a permutációkat, amelyek n különböző elemből állnak össze m elem kiválasztásával, amelyek akár az elemek összetételében, akár sorrendjükben különböznek egymástól, általában elhelyezéseknek nevezik, a permutációk pedig az azonos n különböző elemből álló kombinációk teljes halmazát. elemek és csak elhelyezkedésük sorrendjében különböznek egymástól. Ebben az értelemben egy n különböző elemből álló halmaz összes lehetséges permutációjának számát a Pn = n faktoriális képlet segítségével számítjuk ki! vagy Excelben „=FACT(N)” (lásd: 1. ábra)

Például, ha beírja: „=PERST(3;2)”, 6-ot kapunk. Ez 6 kombináció: (1,2), (2,1), (1,3), (3,1), ( 2,3), (3.2).

De a beépített „=NUMBERCOMB(N;K)” függvény egy kombinatorikus képletet állít elő, amelyet „Kombinációk számának” nevezünk. Az orosz nyelvű irodalomban így nevezik az n különböző elemből összeállított permutációkat, amelyek mindegyike m elemet választ, amelyek csak az elemek összetételében különböznek egymástól, és a kiválasztás sorrendje közömbös (lásd 4. ábra).

A beépített funkciók használatakor használja a Súgót ehhez a funkcióhoz. Például:

Önállóan megoldandó problémák

1. Számolja ki:

2. Számolja ki:

3. Számolja ki:

4. Keresse meg n, ha 5С n 3 =

5. Keresse meg n, Ha

6. Keresse meg n, Ha

7. Keresse meg n, Ha

8. Keresse meg n, Ha ,kn

9. Oldja meg az egyenletet!

10. Oldja meg a rendszert

11. Hány jelet tudsz készíteni 6 különböző színű zászlóból, 2-es csoportokban?

12. Hányféleképpen lehet kilenc jelölt közül négy személyt kiválasztani négy különböző pozícióra?

13. Hány telefonszámot lehet 6 számjegyből összeállítani úgy, hogy minden egyes számban minden számjegy más legyen?

14. Naponta 10 tantárgy és 5 különböző óra van az osztályban. Hányféleképpen oszthatók el az órák egy napon?

15. Hány négyjegyű számot írhat le mind a 10 számjegyből ismétlés nélkül?

16. Egy vállalat kilenc jelölt közül választ ki három különböző pozíciót. Hány módja van ennek a választásnak?

17. Nyolcadik évfolyamon 15 tantárgyat tanulnak. Hányféleképpen készíthet órarendet szerdára, ha tudja, hogy ezen a napon 6 tanórának kell lennie?

18. Az országos labdarúgó-bajnokság élvonalában 16 csapat szerepel. A harc az arany-, ezüst- és bronzéremért folyik. Hányféleképpen oszthatók el az érmek a csapatok között?

19. Hányféleképpen lehet 9 embert leültetni egy asztalhoz 9 evőeszközzel?

20. Az ülésen 6 előadó szólal fel. Hányféleképpen rendezhető el a nevük a listában?

21. Hány háromjegyű szám készíthető az 1, 2, 3 számjegyekből, ha minden számjegy csak egyszer szerepel a szám képében?

22. Hányféleképpen lehet 10 különböző könyvet elhelyezni egy polcon úgy, hogy bizonyos 4 könyv egymás mellett álljon?

23. Egyfordulós labdarúgó tornán 8 csapat vesz részt. Hány mérkőzést fognak játszani?

24. A 25 hallgatóból három küldöttet kell kiválasztani a konferenciára. Hányféleképpen lehet ezt megtenni?

25. Hányféleképpen lehet két alkatrészt kiválasztani egy 10 alkatrészt tartalmazó dobozból?

26. Egy pakliban 36 kártya van, ebből 4 ász. Hányféleképpen lehet 6 lapot felhúzni úgy, hogy 2 ász legyen közöttük?

27. Egy összetett csapat két festőből, három vakolóból és egy asztalosból áll. Hány különböző csapat hozható létre egy 15 festőből, 10 vakolóból és 5 asztalosból álló munkacsoportból?

28. A selejtező tornán 10 csapat vesz részt 3 jegyért a világbajnokságra. Hány változata létezik a „szerencsés háromnak”?

29. 12 főből négyet választanak ki 4 azonos pozícióra. Hányféleképpen lehet ilyen választást meghozni?

30. Hányféleképpen lehet összeállítani egy 3 katonából és egy parancsnokból álló felderítő csoportot, ha 12 katonából és 3 parancsnokból áll?

31. A repülőn adott n amelyeknek három pontja nincs ugyanazon az egyenesen. Határozza meg a pontok páros összekapcsolásával elérhető egyenesek számát!

32. A morze betűk pontok és kötőjelek sorozataként jönnek létre. Hány különböző betűt lehet alkotni 5 jelből?

33. Hány különböző hétjegyű telefonszám létezik?

34. Egy bizonyos ábécé betűit pontok, kötőjelek és szóközök sorozataként alakítsuk ki. Hány különböző betűt lehet alkotni 5 jelből?

35. Bridzs közben egy 52 lapból álló kártyapaklit osztanak szét négy játékos között, minden játékosnak 13 kártyával. Hány különböző módja van a kártyaosztásnak?

36. A posta ötféle képeslapot értékesít. Határozza meg, hány módon vásárolhat hét képeslapot.

37. Két gyűjtő bélyeget cserél. Határozza meg a cseremódok számát, ha az első gyűjtő 3 bélyeget cserél, a második pedig 6 bélyeget. (A csere egy bélyegre történik).

38. Az egyik tanulónak 6 matematikai könyve van, a másiknak 5. Hányféleképpen cserélhetik ki az egyik 2 könyvét egy másik 2 könyvére?

39. Hányféle betűváltoztatás lehetséges a következő szavakban: „zár”, „rotor”, „védekezés”, „harang”, „szeminárium”?

40. Hányféleképpen helyezhető el 9 cellába a következő 9 betű: a, a, a, b, b, b, c, c, c?

41. A kocsiban 6 ülés van. Hányféleképpen ülhet be 6 ember ebbe az autóba, ha csak ketten ülhetnek be a vezetőülésbe?

42. Hányféleképpen lehet egy 52 lapból álló pakliból 6 ászt és királyt tartalmazó, azonos színû kártyát húzni?

43. Határozza meg a bővítést n=5 esetén!

44. Határozza meg a bővítést n=8 esetén!

45. Keress olyan tagot a bővítésben, amelyik nem tartalmazza x-et (vagyis x-et nulladik hatványig).

46. ​​Keresse meg a hatodik bővítési tagot , ha a végétől számított harmadik tag binomiális együtthatója 45.

47. Bomlásban a harmadik tag együtthatója 44-gyel nagyobb, mint a második tag együtthatója. Keresse meg a szabad tagot, vagyis azt a bővítési tagot, amely nem függ x-től (az x-től nem függő tag lesz az, amelyik nulladik hatványig tartalmazza az x-et).

48. A binomiális bővítésben találjon olyan kifejezéseket, amelyek nem tartalmaznak irracionalitást.

49. Keresse meg a bővítési tag számát , amely egyenlő hatványú a-t és b-t tartalmaz.

2. számú gyakorlati óra

(interaktív óra kiscsoportokban)

Boole-függvények

Az óra célja: tudjon különféle Boole-függvényeket szerkeszteni, ellenőrizze a Boole-képletek ekvivalenciáját (az igazságtáblázat segítségével), meghatározza a lényeges és fiktív változókat.

Tanterv:

1. Alapműveletek

2. Boole-függvények n változóból

3. Alapvető egyenértékűségek

Meg kell jegyezni, hogy a kombinatorika a felsőbb matematika önálló ága (és nem része a tervnek), és erről a tudományágról komoly tankönyvek születtek, amelyek tartalma időnként nem egyszerűbb, mint az absztrakt algebra. Az elméleti ismeretek egy kis része azonban nekünk is elég lesz, és ebben a cikkben megpróbálom hozzáférhető formában elemezni a téma alapjait tipikus kombinatorikai problémákkal. És sokan segíteni fognak nekem ;-)

Mit fogunk csinálni? Szűk értelemben a kombinatorika egy bizonyos halmazból létrehozható különféle kombinációk kiszámítása diszkrét tárgyakat. Tárgy alatt minden elszigetelt tárgy vagy élőlény értendő – emberek, állatok, gombák, növények, rovarok stb. Ugyanakkor a kombinatorikát egyáltalán nem érdekli, hogy a készlet egy tányér búzadarából, egy forrasztópáka és egy mocsári békából áll. Alapvetően fontos, hogy ezeket a tárgyakat fel lehessen sorolni – három van belőlük (diszkrét)és az a fontos, hogy egyik sem egyforma.

Sok mindennel foglalkoztunk, most a kombinációkkal. A kombinációk leggyakoribb típusai az objektumok permutációi, halmazból való kiválasztása (kombináció) és elosztása (elhelyezés). Lássuk, hogyan történik ez most:

Permutációk, kombinációk és elhelyezések ismétlés nélkül

Ne féljen a homályos kifejezésektől, különösen azért, mert néhányuk valóban nem túl jó. Kezdjük a cím végével – mit jelent? nincs ismétlés"? Ez azt jelenti, hogy ebben a részben olyan halmazokat fogunk megvizsgálni, amelyek a következőkből állnak különféle tárgyakat. Például ... nem, nem kínálok kását forrasztópákával és békával, jobb, ha valami finomabb =) Képzeld el, hogy egy alma, egy körte és egy banán került az asztalra előtted ( ha megvannak, a helyzet a valóságban is szimulálható). A gyümölcsöket balról jobbra helyezzük el a következő sorrendben:

alma / körte / banán

Egy kérdés: Hányféleképpen lehet átrendezni?

Az egyik kombinációt már fentebb leírtuk, és a többivel nincs probléma:

alma / banán / körte
körte / alma / banán
körte / banán / alma
banán / alma / körte
banán / körte / alma

Teljes: 6 kombináció vagy 6 permutációk.

Oké, nem volt nehéz felsorolni az összes lehetséges esetet, de mi van, ha több objektum van? Mindössze négy különböző gyümölccsel a kombinációk száma jelentősen megnő!

Nyissa meg a referenciaanyagot (kényelmes kinyomtatni a kézikönyvet)és a 2. pontban keresse meg a permutációk számának képletét.

Gond nélkül – 3 objektumot különböző módokon lehet átrendezni.

Második kérdés: Hányféleképpen választhatsz a) egy gyümölcsöt, b) két gyümölcsöt, c) három gyümölcsöt, d) legalább egy gyümölcsöt?

Miért érdemes választani? Tehát az előző pontban feldobtuk az étvágyat - enni! =)

a) Egy gyümölcsöt természetesen háromféleképpen lehet kiválasztani – vegyünk almát, körtét vagy banánt. A formális számítás a szerint történik a kombinációk számának képlete:

A bejegyzést ebben az esetben a következőképpen kell érteni: "Hányféleképpen választhatsz ki egy gyümölcsöt a háromból?"

b) Soroljuk fel két gyümölcs összes lehetséges kombinációját:

alma és körte;
alma és banán;
körte és banán.

A kombinációk száma könnyen ellenőrizhető ugyanazzal a képlettel:

Hasonlóan értelmezhető a szócikk: „hányféleképpen lehet kiválasztani 2 gyümölcsöt a háromból?”

c) És végül, csak egyféleképpen választhat három gyümölcsöt:

Egyébként a kombinációk számának képlete értelmes marad egy üres mintánál:
Ily módon egyetlen gyümölcsöt sem választhat – sőt, semmit sem vesz, és ennyi.

d) Hányféleképpen szedheti legalább egy gyümölcs? A „legalább egy” feltétel azt jelenti, hogy elégedettek vagyunk 1 gyümölccsel (bármelyik), vagy bármelyik 2 gyümölccsel, vagy mind a 3 gyümölccsel:
ezekkel a módszerekkel kiválaszthat legalább egy gyümölcsöt.

Azok az olvasók, akik alaposan áttanulmányozták a bevezető leckét Valószínűségi elmélet, már sejtettünk valamit. De a pluszjel jelentéséről később.

A következő kérdés megválaszolásához két önkéntesre van szükségem... ...Nos, mivel senki sem akar, akkor hívlak a testületbe =)

Harmadik kérdés: Hányféleképpen oszthatsz ki egy-egy gyümölcsöt Dashának és Natasának?

Két gyümölcs kiosztásához először ki kell választani őket. Az előző kérdés „be” bekezdése szerint ezt többféleképpen is meg lehet tenni, átírom őket:

alma és körte;
alma és banán;
körte és banán.

De most kétszer annyi kombináció lesz. Vegyük például az első gyümölcspárt:
Dashát almával, Natasát pedig körtével kezelheti;
vagy fordítva – Dasha kapja a körtét, Natasa pedig az almát.

És egy ilyen permutáció minden gyümölcspárnál lehetséges.

Vegyük ugyanazt a diákcsoportot, amelyik elment a táncba. Hányféleképpen párosítható egy fiú és egy lány?

Bizonyos módokon kiválaszthat 1 fiatalembert;
módokon választhat 1 lányt.

Így egy fiatalember És Választhatsz egy lányt: módokon.

Ha minden halmazból 1 objektumot választunk ki, a következő kombinációk számlálási elve érvényes: " minden egy halmazból egy tárgy alkothat egy párt mindegyikkel egy másik halmaz tárgya."

Vagyis Oleg a 13 lány közül bármelyiket meghívhatja táncolni, Jevgenyi is a tizenhárom közül bármelyiket, és a többi fiatalnak is hasonló választása van. Összesen: lehetséges párok.

Meg kell jegyezni, hogy ebben a példában a pár kialakulásának „története” nem számít; viszont ha a kezdeményezést is figyelembe vesszük, akkor a kombinációk számát meg kell duplázni, hiszen a 13 lány mindegyike bármelyik fiút meghívhatja táncolni. Minden az adott feladat körülményeitől függ!

Hasonló elv érvényes a bonyolultabb kombinációkra is, például: hányféleképpen lehet kiválasztani két fiatalembert? És két lány részt venni egy KVN-skitben?

Unió ÉS egyértelműen utal arra, hogy a kombinációkat meg kell szorozni:

Lehetséges művészcsoportok.

Más szavakkal, minden egyes egy fiúpár (45 egyedi pár) léphet fel Bármi egy pár lány (78 egyedi pár). És ha figyelembe vesszük a szereposztást a résztvevők között, akkor még több kombináció lesz. ...nagyon szeretném, de továbbra is tartózkodom a folytatástól, hogy ne keltsek benned idegenkedést a diákélettől =).

A kombinációk szorzására vonatkozó szabály nagyobb számú szorzóra is vonatkozik:

8. probléma

Hány olyan háromjegyű szám van, amely osztható 5-tel?

Megoldás: az érthetőség kedvéért jelöljük ezt a számot három csillaggal: ***

BAN BEN százas hely Bármelyik számot beírhatja (1, 2, 3, 4, 5, 6, 7, 8 vagy 9). A nulla nem megfelelő, mivel ebben az esetben a szám már nem háromjegyű.

De tízes hely("középen") 10 számjegy közül választhat: .

A feltétel szerint a számnak oszthatónak kell lennie 5-tel. Egy szám osztható 5-tel, ha 5-re vagy 0-ra végződik. Így a legkisebb jelentőségű számjegyben megelégszünk 2 számjeggyel.

Összességében van: 5-tel osztható háromjegyű számok.

Ebben az esetben a mű megfejtése a következőképpen történik: „9 módon választhat számot százas hely És 10 módszer a szám kiválasztására tízes hely És 2 út befelé egységek számjegy»

Vagy még egyszerűbben: " minden egyes 9 számjegytől ig százas hely egyesíti mindegyikkel 10 számjegyből áll tízes hely és mindegyikkel két számjegytől ig egységek számjegy».

Válasz: 180

És most…

Igen, majdnem megfeledkeztem az 5. feladathoz beígért kommentárról, amelyben Bornak, Dimának és Volodjának különböző módon oszthatnak egy-egy lapot. A szorzás itt ugyanazt jelenti: 3 kártya eltávolításának módjai a pakliból ÉS az összesben minta rendezze át őket módokon.

És most egy egyedül megoldandó probléma... most kitalálok valami érdekesebbet... legyen szó a blackjack ugyanarról az orosz változatáról:

9. probléma

Hány nyerő kombináció van 2 lapból a "pont" kijátszásakor?

Aki nem tudja: a nyerő kombináció 10 + ACE (11 pont) = 21 pont, és nézzük a két ász nyerő kombinációját.

(a kártyák sorrendje minden párban nem számít)

Rövid megoldás és válasz a lecke végén.

Egyébként ne tekintsd primitívnek a példát. A blackjack szinte az egyetlen olyan játék, amelyhez létezik matematikai alapú algoritmus, amely lehetővé teszi a kaszinó legyőzését. Az érdeklődők könnyedén találhatnak rengeteg információt az optimális stratégiáról és taktikáról. Igaz, az ilyen mesterek gyorsan az összes intézmény feketelistájára kerülnek =)

Itt az ideje, hogy egy pár szilárd feladattal lefedett anyagot összevonjuk:

10. probléma

Vasyának 4 macskája van otthon.

a) Hányféleképpen lehet macskákat leültetni a szoba sarkaiba?
b) hányféleképpen engedheti el a macskákat sétálni?
c) Vasya hányféleképpen tud felvenni két macskát (az egyiket a balján, a másikat a jobbján)?

Döntsünk: először is ismét figyelni kell arra, hogy a probléma foglalkozik különböző tárgyakat (még akkor is, ha a macskák egypetéjű ikrek). Ez nagyon fontos feltétel!

a) A macskák csendje. Ennek a végrehajtásnak megfelelően az összes macska egyszerre
+ a helyük fontos, ezért itt vannak permutációk:
ezekkel a módszerekkel elhelyezheti a macskákat a szoba sarkaiban.

Ismétlem, hogy a permutálásnál csak a különböző objektumok száma és egymáshoz viszonyított helyzete számít. Vasya hangulatától függően félkörben ültesse le az állatokat a kanapéra, egy sorba az ablakpárkányra stb. – minden esetben 24 permutáció lesz, az érdeklődők a kényelem kedvéért elképzelhetik, hogy a macskák sokszínűek (például fehér, fekete, piros és cirmos) és felsorolják az összes lehetséges kombinációt.

b) Hányféleképpen engedheti el a macskákat sétálni?

Feltételezik, hogy a macskák csak az ajtón keresztül mennek sétálni, és a kérdés közömbösséget jelent az állatok számát illetően - 1, 2, 3 vagy mind a 4 macska mehet sétálni.

Számolunk minden lehetséges kombinációt:

Olyan módokon, ahogy egy macskát (a négy közül bármelyiket) elengedhet sétálni;
hogyan engedhet el két macskát sétálni (sorolja fel maga a lehetőségeket);
oly módon, hogy három macskát elengedhet sétálni (a négy közül az egyik otthon ül);
Így elengedheti az összes macskát.

Valószínűleg úgy gondolta, hogy a kapott értékeket összegezni kell:
hogyan engedheti el a macskákat sétálni.

A rajongók számára a probléma bonyolult változatát ajánlom – amikor bármely mintában bármelyik macska véletlenszerűen ki tud lépni, mind az ajtón, mind az ablakon a 10. emeleten. Érezhetően megnövekszik a kombinációk száma!

c) Vasya hányféleképpen tud felvenni két macskát?

A helyzet abból áll, hogy nem csak 2 állatot kell kiválasztani, hanem mindkét kézbe kell helyezni:
Ilyen módon 2 macskát vehet fel.

Második megoldás: módszerekkel választhat két macskát Ésültetési módok minden egy pár kéznél:

Válasz: a) 24, b) 15, c) 12

Nos, hogy megtisztítsa a lelkiismeretét, valami konkrétabbat a kombinációk szorzásáról... Hagyjon Vasyának 5 további macskája =) Hányféleképpen engedhet el 2 macskát sétálni? És 1 macska?

Vagyis azzal minden egyes pár macska szabadon engedhető minden macska.

Egy másik gombos harmonika az önálló megoldáshoz:

11. probléma

Három utas szállt fel egy 12 emeletes épület liftjébe. Mindenki, a többiektől függetlenül, azonos valószínűséggel bármelyik (a 2. emelettől kezdve) kiléphet. Hányféleképpen:

1) az utasok ugyanazon az emeleten szállhatnak le (a kilépési sorrend nem számít);
2) az egyik emeleten két ember szállhat le, a másikon egy harmadik;
3) az emberek különböző emeleteken léphetnek ki;
4) Az utasok kiszállhatnak a liftből?

És itt gyakran újra kérdeznek, pontosítok: ha 2-3 ember kilép ugyanazon az emeleten, akkor a kilépés sorrendje nem számít. GONDOLKODJ, használj képleteket és szabályokat a kombinációk összeadásához/szorzásához. Nehézségek esetén hasznos, ha az utasok nevet adnak, és találgatnak, milyen kombinációkkal szállhatnak ki a liftből. Nem kell felháborodni, ha valami nem sikerül, például a 2. pont elég alattomos.

Teljes megoldás részletes megjegyzésekkel a lecke végén.

Az utolsó bekezdés a szintén elég gyakran előforduló kombinációknak szól - szubjektív értékelésem szerint a kombinatorikai problémák körülbelül 20-30%-ában:

Permutációk, kombinációk és elhelyezések ismétlésekkel

A felsorolt ​​kombinációtípusokat a referenciaanyag 5. bekezdése vázolja A kombinatorika alapképletei némelyik azonban első olvasatra nem teljesen egyértelmű. Ebben az esetben célszerű először gyakorlati példákkal megismerkedni, és csak azután megérteni az általános megfogalmazást. Megy:

Permutációk ismétlésekkel

Az ismétléses permutációkban, mint a „hétköznapi” permutációkban, mind a sok tárgyat egyszerre, de van egy dolog: ebben a halmazban egy vagy több elem (objektum) ismétlődik. Teljesítse a következő szabványt:

12. probléma

Hány különböző betűkombinációt kaphatunk a következő betűket tartalmazó kártyák átrendezésével: K, O, L, O, K, O, L, b, Ch, I, K?

Megoldás: abban az esetben, ha az összes betű különbözik, akkor egy triviális képletet kell alkalmazni, de teljesen egyértelmű, hogy a javasolt kártyakészletnél bizonyos manipulációk „tétlenül” működnek, például ha két kártyát felcserél a „K” betűkkel bármelyik szóban ugyanazt a szót kapja. Sőt, a kártyák fizikailag nagyon különbözőek lehetnek: az egyik lehet kerek, rányomtatva a „K” betűvel, a másik lehet négyzet alakú „K” betűvel. De a feladat jelentése szerint akár olyan kártyákat is azonosnak tekintendők, mivel a feltétel a betűkombinációkra kérdez rá.

Minden rendkívül egyszerű - csak 11 kártya, beleértve a levelet:

K – 3-szor ismételve;
O – 3-szor ismételve;
L – 2-szer ismételve;
b – 1-szer ismételve;
H – 1-szer ismételve;
És - ismételve 1 alkalommal.

Ellenőrzés: 3 + 3 + 2 + 1 + 1 + 1 = 11, amit ellenőrizni kellett.

A képlet szerint permutációk száma ismétlésekkel:
különböző betűkombinációkat kaphatunk. Több mint félmillió!

A nagy faktorérték gyors kiszámításához kényelmesen használható a szabványos Excel-függvény: írja be bármelyik cellába =TÉNY(11)és nyomja meg Belép.

A gyakorlatban teljesen elfogadható, ha nem írjuk le az általános képletet, és ezen kívül elhagyjuk az egységfaktorokat:

De az ismételt levelekkel kapcsolatban előzetes észrevételek szükségesek!

Válasz: 554400

Az ismétléssel járó permutációk másik tipikus példája a sakkfigurák elhelyezési problémája, amely a raktárban található kész megoldások a megfelelő pdf-ben. Az önálló megoldáshoz pedig egy kevésbé képletes feladattal álltam elő:

13. probléma

Alexey sportol, heti 4 napot atlétikáz, 2 napot - erőgyakorlatokat és 1 napot pihen. Hányféleképpen tud heti beosztást készíteni magának?

A képlet itt nem működik, mert figyelembe veszi a véletlen cseréket (például a szerdai erőgyakorlatok felcserélése a csütörtöki erőgyakorlatokkal). És még egyszer - valójában ugyanaz a 2 erősítő edzés nagyon eltérhet egymástól, de a feladat kontextusában (az ütemezés szempontjából) ugyanazoknak az elemeknek minősülnek.

Kétsoros megoldás és válasz a lecke végén.

Kombinációk ismétlésekkel

Az ilyen típusú kombinációk jellemzője, hogy a mintát több csoportból veszik, amelyek mindegyike azonos objektumokból áll.

Mindenki keményen dolgozott ma, így ideje felfrissülni:

14. probléma

A diákmenzán tésztás kolbászt, sajttortát és fánkot árulnak. Hányféleképpen vásárolhat öt pitét?

Megoldás: azonnal ügyeljen az ismétlődéses kombinációk tipikus kritériumára - a feltétel szerint nem objektumok halmazát kínálják választásra, hanem különböző fajták tárgyak; Feltételezzük, hogy legalább öt hot dogot, 5 sajttortát és 5 fánkot kínálnak. Az egyes csoportok pitékje természetesen más - mert abszolút egyforma fánkokat csak számítógépen lehet szimulálni =) A piték fizikai jellemzői azonban nem jelentősek a probléma szempontjából, és a virsli / sajttorta / a csoportjukba tartozó fánk azonosnak számít.

Mi lehet a mintában? Először is meg kell jegyezni, hogy biztosan lesznek egyforma piték a mintában (mivel 5 darabot választunk, és 3 féle közül lehet választani). Itt minden ízléshez van lehetőség: 5 hot dog, 5 sajttorta, 5 fánk, 3 hot dog + 2 sajttorta, 1 hot dog + 2 sajttorta + 2 fánk stb.

A „szokásos” kombinációkhoz hasonlóan a piték kiválasztásának és elhelyezésének sorrendje nem számít - csak kiválasztott 5 darabot, és kész.

A képletet használjuk kombinációk száma ismétléssel:
Ezzel a módszerrel 5 pitét vásárolhat.

Jó étvágyat kívánunk!

Válasz: 21

Milyen következtetés vonható le számos kombinatorikus problémából?

Néha a legnehezebb az állapot megértése.

Hasonló példa egy független megoldásra:

15. probléma

A pénztárca meglehetősen sok 1, 2, 5 és 10 rubeles érmét tartalmaz. Hányféleképpen lehet három érmét kivenni egy pénztárcából?

Önkontroll céljából válaszoljon néhány egyszerű kérdésre:

1) Eltérhet a mintában szereplő összes érme?
2) Nevezze meg a „legolcsóbb” és „legdrágább” érmék kombinációját!

Megoldás és válaszok a lecke végén.

Személyes tapasztalataim alapján elmondhatom, hogy az ismétléses kombinációk a legritkább vendég a gyakorlatban, ami nem mondható el a következő típusú kombinációkról:

Elhelyezések ismétlésekkel

Egy elemekből álló halmazból elemek kerülnek kiválasztásra, és az egyes kijelöléseknél fontos az elemek sorrendje. És minden rendben is lenne, de elég váratlan poén, hogy az eredeti készlet bármelyik tárgyát annyiszor választhatjuk ki, ahányszor csak akarjuk. Képletesen szólva: „a sokaság nem fog csökkenni”.

Mikor történik ez? Tipikus példa a több lemezes kombinációs zár, de a technológiai fejlődés miatt célszerűbb ennek digitális leszármazottját figyelembe venni:

16. probléma

Hány négyjegyű PIN kód van?

Megoldás: valójában a probléma megoldásához elegendő a kombinatorika szabályainak ismerete: bizonyos módokon kiválaszthatja a PIN kód első számjegyét És módok - a PIN-kód második számjegye És annyiféleképpen – harmadik És ugyanaz a szám - a negyedik. Így a kombinációk szorzása szabálya szerint egy négyjegyű pin kódot a következőképpen lehet összeállítani: módokon.

És most a képlet segítségével. A feltételnek megfelelően felkínálunk egy számkészletet, amelyből kiválasztjuk és rendezzük a számokat egy bizonyos sorrendben, míg a mintában szereplő számok megismétlődhetnek (azaz az eredeti halmaz bármely számjegye tetszőleges számú alkalommal használható). Az ismétléses elhelyezések számának képlete szerint:

Válasz: 10000

Mi jut itt eszembe... ...ha az ATM a harmadik sikertelen PIN kód beírási kísérlet után „megeszi” a kártyát, akkor a véletlenszerű felvételre nagyon kicsi az esély.

És ki mondta, hogy a kombinatorikának nincs gyakorlati jelentése? Kognitív feladat az oldal minden olvasójának:

17. probléma

Az állami szabvány szerint az autó rendszáma 3 számból és 3 betűből áll. Ebben az esetben a három nullát tartalmazó szám elfogadhatatlan, és a betűk az A, B, E, K, M, N, O, P, S, T, U, X halmazból kerülnek kiválasztásra. (csak azokat a cirill betűket használjuk, amelyek helyesírása egybeesik a latin betűkkel).

Hány különböző rendszámot lehet létrehozni egy régióhoz?

Egyébként nincs belőlük olyan sok. Nagy régiókban nincs elegendő ilyen mennyiség, ezért számukra több kód létezik a RUS felirathoz.

A megoldás és a válasz a lecke végén található. Ne felejtsd el használni a kombinatorika szabályait ;-) ...meg akartam mutatni, hogy mi az exkluzív, de kiderült, hogy nem exkluzív =) Megnéztem a Wikipédiát - ott vannak számítások, bár kommentár nélkül. Bár oktatási célból valószínűleg kevesen oldották meg.

Izgalmas leckénk a végéhez ért, és végül szeretném elmondani, hogy nem vesztegette az idejét – azért, mert a kombinatorikai képletek egy másik létfontosságú gyakorlati alkalmazást találnak: különféle problémákban találhatók Valószínűségi elmélet,
és be a valószínűség klasszikus meghatározásával kapcsolatos problémák- különösen gyakran =)

Köszönjük mindenkinek az aktív részvételt és hamarosan találkozunk!

Megoldások és válaszok:

2. feladat: Megoldás: keresse meg 4 kártya összes lehetséges permutációjának számát:

Ha egy nullát tartalmazó kártya kerül az 1. helyre, a szám háromjegyűvé válik, ezért ezeket a kombinációkat ki kell zárni. Legyen a nulla az 1. helyen, majd az alsó számjegyek maradék 3 számjegye különböző módokon átrendezhető.

jegyzet : mert Mivel csak néhány kártya van, könnyű felsorolni az összes lehetőséget itt:
0579
0597
0759
0795
0957
0975

Így a javasolt készletből elkészíthetjük:
24 – 6 = 18 négyjegyű szám
Válasz : 18

4. feladat: Megoldás: bizonyos módokon 3 kártyát választhatsz a 36-ból.
Válasz : 7140

6. feladat: Megoldás: módokon.
Egy másik megoldás : hogyan választhat ki két személyt a csoportból és és
2) A „legolcsóbb” készlet 3 rubelt tartalmaz, a „legdrágább” pedig 3 tízrubeles érmét.

17. probléma: Megoldás: ezekkel a módszerekkel létrehozhat egy autószám digitális kombinációját, miközben az egyiket (000) ki kell zárni: .
ezekkel a módszerekkel létrehozhatja a rendszám betűkombinációját.
A kombinációk szorzására vonatkozó szabály szerint a teljes összeg a következő:
rendszámtáblák
(minden egyes digitális kombináció kombinálva van mindegyikkel betűkombináció).
Válasz : 1726272